SoySim: A Simulation Model for Soybean Growth and Yield
Tri D. Setiyono, Kenneth G. Cassman, James E. Specht, Albert Weiss, Achim Dobermann, Haishun Yang
Department of Agronomy and Horticulture, Institute of Agriculture and Natural Resources
2010 by University of Nebraska-Lincoln. All rights reserved
![]()
Contents
1. Yield Potential and Yield Gaps
2.4.1. Sources of Weather Data
2.4.2.1 Manual editing of weather file:
2.4.2.2 Downloading and conversion of weather data
2.4.2.3 Importing weather data from the Hybrid-maize model
3. Detailed Information about the SoySim Model
3.3. Dry matter accumulation and partitioning
3.5. Uncertainties and Future Improvements
1. Yield Potential and Yield Gaps
Yield potential is defined as yield of a cultivar when grown in environments at which it is adapted with nutrients and water not limited, and pests, diseases, lodging, and weeds controlled (1993). Hence, for a given crop variety in a specific growth environment, yield potential is determined by the amount of incident solar radiation, temperature, daylength, and plant densitythe latter determining the rate at which the leaf canopy develops under a given solar radiation and temperature regime. The difference between yield potential and the actual yield represents the exploitable yield gap (Fig. 1.1). Hence, genotype, solar radiation, temperature, daylength, plant population, and degree of water deficit determine water-limited yield potential. In addition to yield reduction from limited water supply, actual farm yields are determined by the magnitude of yield reduction or loss from other factors such as nutrient deficiencies or imbalances, poor soil quality, root and/or shoot diseases, insect pests, weed competition, excessive water, and lodging.
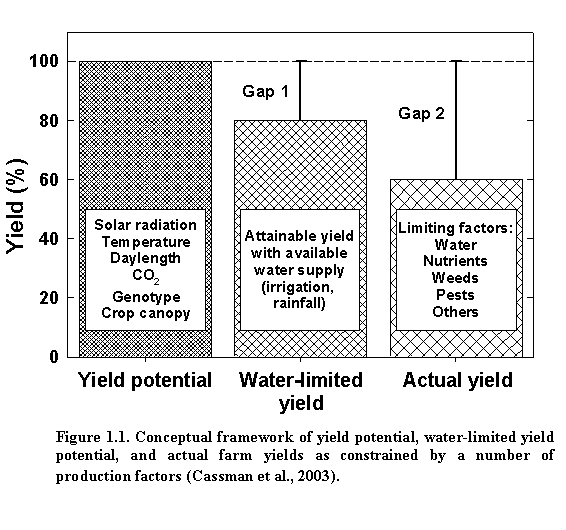
Management decisions such as cultivar selection, planting date, and plant density can affect the yield potential at a given site by influencing the utilization of available solar radiation and soil moisture reserves during the growing season. Yield potential also fluctuates somewhat from year to year (typically 10-15%) because of normal variation in solar radiation and temperature regime. To achieve yield potential, the crop must be optimally supplied with water and nutrients and completely protected against weeds, pests, diseases, and other factors that may reduce growth. Such conditions are rarely achieved under field conditions, nor is it likely to be cost-effective for farmers to strive for such perfection in management. Instead, understanding site yield potential and its normal year-to-year variation can help identify management options and input requirements that combine to reduce the size of the exploitable yield gap, while maintaining profitable and highly efficient production practices.
For much of the U.S. Corn-Soybean Belt, available moisture is the most important growth-limiting factor. The water deficit is determined by factors such as soil water holding capacity, rainfall, irrigation, and evapotranspiration, which vary from site to site and year to year. Because irrigation can help ensure adequate water supply in the face of suboptimal rainfall, differences between yield potential and water-limited yield (yield gap 1 in Fig. 1.1.) are smaller and less variable in irrigated systems compared to rainfed soybean systems.
In well-managed irrigated soybean fields/systems, the attainable water-limited yield is close to the yield potential ceiling and relatively stable from year to year, because irrigation is provided during key growth stages to make up for water deficits. Management can therefore focus on providing sufficient nutrients to fully exploit attainable yield and on minimizing yield-reducing factors that determine yield gap 2 shown in Fig. 1.1. In rainfed soybean fields/systems, the attainable water-limited yield is typically less than that for irrigated soybean fields/systems, but fluctuates widely, depending on the initial soil moisture status, soil water holding capacity, planting date, plant density, evapotranspiration, and rainfall during the growing season. Therefore, setting a realistic yield goal is more difficult in rainfed systems than under irrigated conditions because both yield gaps 1 and 2 can vary greatly from site to site or year to year.
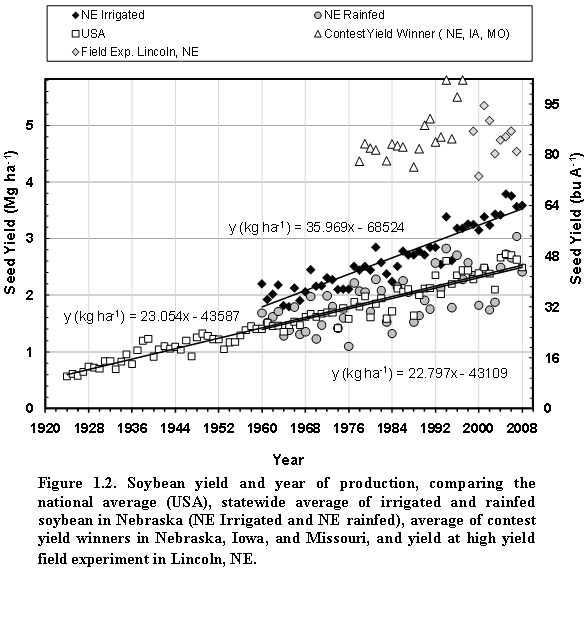
Generally, average soybean yields in the past four decades have risen steadily due to genetic and agronomic improvements, and a rise in ambient CO2 concentration (Specht et al., 1999), but they do not reflect the yield potential. An alternative measure for the latter are the yields in well- managed field experiments or those of the winners of the annual yield contests, which typically represent combinations of optimal management and favorable weather (Fig. 1.2). The long-term statewide average yield in Nebraska showed that year-to-year variability is substantial and greater in rainfed areas than under irrigated conditions (Fig. 1.2).
Using simplified assumptions of photosynthesis gain and respiration loss of crops that fully cover land, de Wit (1967) calculated the theoretical maximum above ground biomass yields that can be achieved in certain latitudes. For the USA and other production regions with similar latitudes, this maximum biomass accumulation is suggested to be 45 Mg ha-1. Assuming a 50% harvest index, a maximum seed yield ceiling of 22.5 Mg ha-1 is inferred from de Wits theory. Based on this assumption and a 2.8 intrinsic corn to soybean productivity, Specht (1999) suggested a theoretical 8 Mg ha-1 (119 bu A-1) as a yield ceiling for soybeans. The fact that previous high yield studies have not yet exceeded this limit seems to support the validity of this yield limit.
Cooper (2003) suggested that flowering habit is the major barrier for soybean yield potential. Unusually warm temperatures during early growth caused yield to reach a level of 6 mg ha-1 (95.4 bu A-1). It is still uncertain whether such early flowering habit is generally a key factor contributing to the existing gap between yield potential and actual yield. Another obstacle is that in some cases, earlier flowering did not cause higher yield, due to the negative effects of drought and diseases (Cooper, 2003), which indicates that moving yield closer to yield potential will not be as simple as breeding for early flowering traits. Modeling studies can help answer questions about soybean yield limits in interactions with flowering behavior and other factors.
The SoySim model simulates soybean growth on a daily basis from emergence to full maturity (R8). This version of the program simulates soybean yield potential and water use plus irrigation requirements under non-limiting conditions, assuming both optimal nutrient supply and no yield losses from other factors (Fig. 1.1). For simulation of yield potential, the model requires daily weather data for solar radiation and maximum and minimum temperatures. For simulation of the water use and irrigation recommendation, the model requires daily weather data for solar radiation, maximum and minimum temperature, rainfall, reference evapotranspiration, and relative air humidity.
2. Using the SOYSIM Model
2.1. Installation
System requirements:
?????? Free disk space: The software itself requires approximately 3.0 MB space. The actual space required vary depending on weather data files begin used.
?????? Processor: Pentium II minimum, Pentium III or IV recommended
?????? Operating system: Microsoft Windows 95/98/2000/ XP/ Vista
?????? Video: 256 colors at 800 x 600 screen resolution or higher
Installation steps:
?????? Unzip the downloaded file SoysimSetup.zip into a temporary folder on the computer. Then launch the SoySimSetup.exe file and follow the on-screen installation instructions.
The installation procedure will automatically create a shortcut for launching the model on both the desktop and in the Programs list in the Windows Start menu on the lower left corner of the screen.
?
2.2. A Quick Simulation Run
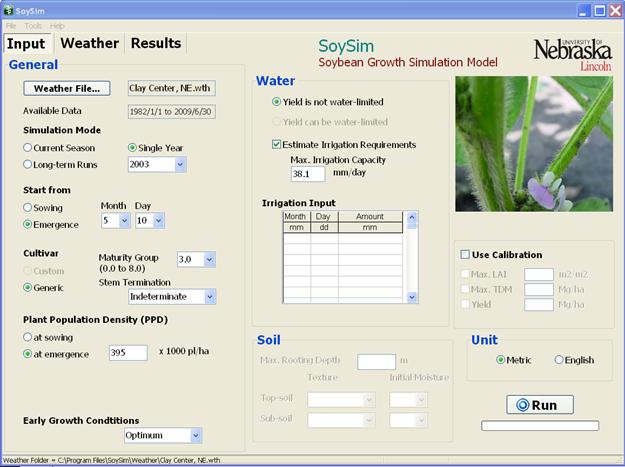
Figure 2.1. SoySim input page after opening weather file for Clay Center, NE and completing other inputs in step 1 in section 2.2.
?
The following example provides an initial trial run with the SOYSIM model with instructions about how to select appropriate input values and how to review the results. We use the default Metric measurement units in this example.
This simulation example simulates soybean growth and yield potential (yield with optimal irrigation and nutrient supply) at Clay Center in south-central Nebraska in a single year (2003). Optimal irrigation is provided throughout crop growth whenever rainfall does not meet crop water requirements. The soybean cultivar has a maturity group rating 3.0 and indeterminate stem termination type.
1.???? Launch the SoySim program by clicking on the desktop icon or selecting it from the Start menu. Enter all model inputs based on the description below. Measurement units can be adjusted to either Metric or English units by clicking the option toggle on the right bottom corner of input page (the first page that appears when starting the SoySim program, Fig. 2.1). In version 2009.1, only the General Input section is applicable (under the single-year option, the calibration option is also applicable). Options in the Water and Soil sections are not available, as this version only simulates yield without water and nutrient limitation.
In the General Input section, select the weather file for this site by clicking on the Weather file button. Browse and choose the file for Clay Center, NE.wth. Select Single year as simulation mode and select 2003 from the drop-down list of available years. For Start from, use the default option Emergence and enter 5 as month and 10 as day for a May 1 emergence date. Emergence is defined as the stage at which at least 50% of the soybean plants are showing their cotyledons above the soil surface. To see the definition and illustration of emergence, double click on the Emergence button. Emergence is the recommended starting option, especially when a reliable record of this stage is available. The option of Start from Sowing should be used with caution, considering the possible inaccuracy of emergence date simulation due to factors not considered in the simulation such as non-optimum (too dry or wet) of soil moisture, compaction, and extreme soil temperature. The default sowing depth is set at 3.00 cm (1.18 inches). The sowing depth can be changed according the actual depth applied. Generally, the deeper the soil depth, the longer it takes for seedlings to emerge. For Maturity Group, select the default 3.0; likewise with the Stem Termination, keep with the default selection of Indeterminate. A pop-up message will appear to confirm the selection when the user attempts to select Semi-determinate. For Plant population density, change the default value of 300 to 395 (=395,000 plants/ha, = 160,000 plants/acre). Leave the Early Growth Condition option at optimum. Non-optimum (medium or poor) early growth conditions limit early soybean leaf development and later tend to also limit final biomass growth and yield.
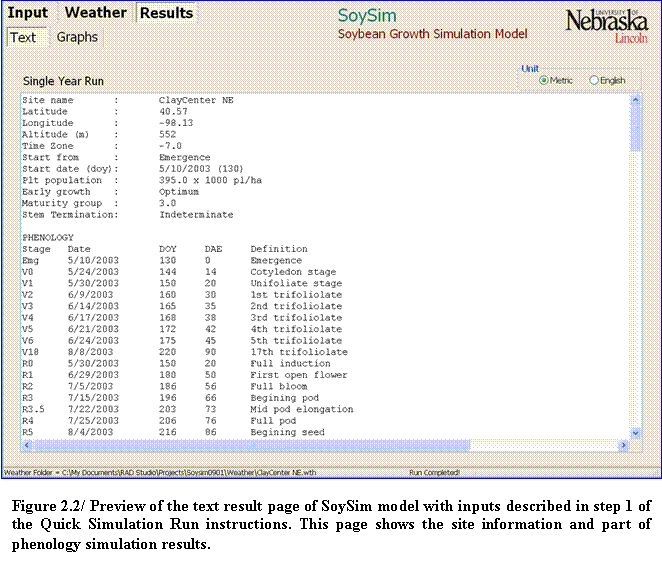
2.???? Verify all entries. Click on the Run button in the lower right corner of the screen. The page display will switch to Text Result (text output) page as soon as the simulation is complete.
3.???? Information about the input of the simulation is given on the top of the Text Result page. This also includes the site information determined on the weather file (Fig. 2.2).
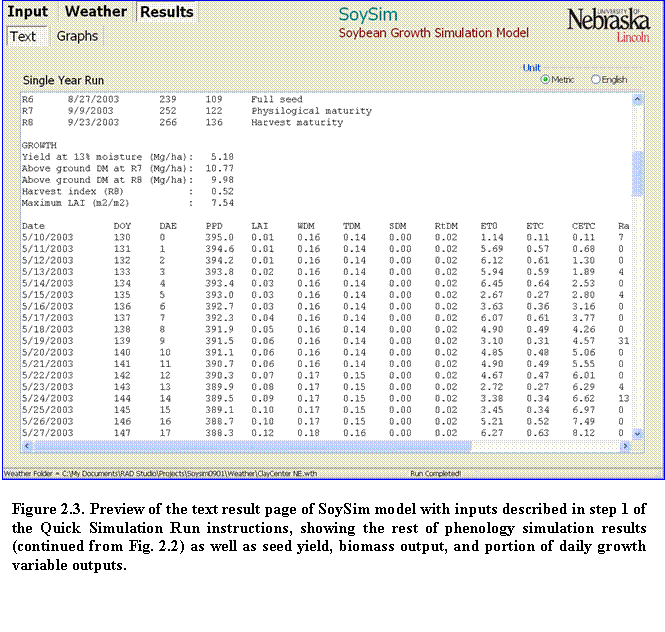
4.???? The next section is a summary of phenology stages. Scroll down the output page to view the rest of the output information, including the simulated seed yield (13% moisture content) and above ground dry matter, as well as daily growth variables from emergence to full maturity (Fig. 2.3). Variables definitions follow at the end of the daily growth variables output. In this example the simulated seed yield is 5.18 Mg/ha (82.4 bu/A).
?
5.???? Click the Graphs tab to view the graphical representation of the simulation outputs (Fig. 2.4).
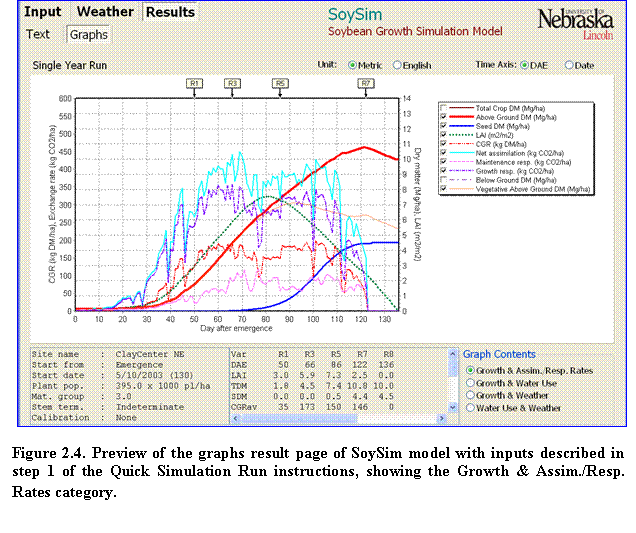
To show or hide an item in the graph, click the corresponding items legend to the right of the graph panel. Click options buttons on the lower right corner of the graph page to change the category of the graph content. The content category options are as follows:
a.????? Growth & Assim./ Resp. Rates. When this category is selected, important growth and intermediate rate variables can be displayed on the graph, including: total crop dry matter, total above ground dry matter, seed dry matter, leaf area index (LAI), crop growth rate (CGR), net assimilation rate, maintenance respiration rate, growth respiration rate, below ground dry matter, and vegetative dry matter.
b.???? Growth & Water Use. When this category is selected, water use related variables can be displayed in the graph in conjunction with the growth variables in a. The water use related variables include the cumulative values of evapotranspiration, effective water input, rain, and recommended irrigation, and the daily value of rain and recommended irrigation.
c.????? Growth & Weather. When this category is selected, weather variables can be displayed in the graph in conjunction with the growth variable in a. Weather variables include daily average, maximum and minimum temperature, solar radiation, relative humidity, and reference evapotranspiration.
d.???? Water User & Weather. When this category is selected, all water use related variables in b can be displayed in conjunction with the weather variables in c.
A summary of the inputs information is shown at the bottom left panel of the Graph page, while the bottom center panel displays average values of relevant variables, depending on the selected Graph Content category, within a given range of phenological stages. Scroll down to the bottom of this panel to see the definitions of the abbreviations used. As a reference, key reproductive stages are shown at the top of the graph panel. At any time, the unit in the graph can be changed from Metric to English or vice versa. Likewise, the time axis can be changed from day after emergence (DAE) to calendar date and vice versa.
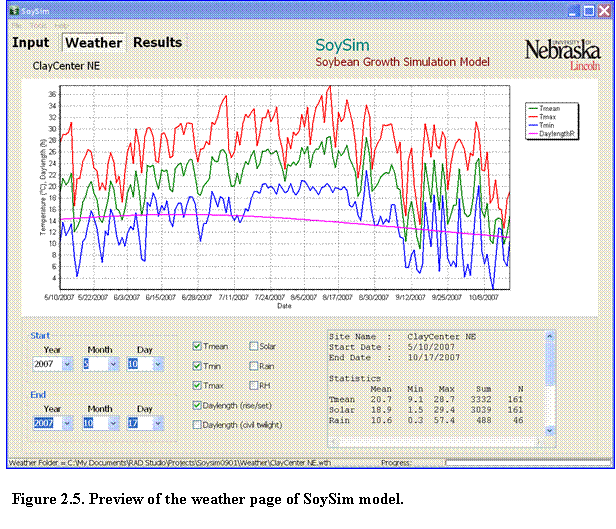
The SoySim model allows users to plot weather variables for a given weather station, regardless of the simulation or without running the growth simulation (Fig. 2.5).
Once a weather station is selected, users can click on the Weather page tab to view the weather graphs. Starting and ending date of the weather data to graph can be selected as desired and the user can select weather variables to view graphically. The panel at the botom right provides statistical values of the weather variables for a given range. Note that statistical values are only shown for the range less than 365 days. The graph itself can display weather variables across years or multiple years.
6.???? To quit the program, either click the X in the upper right corner of the window, or go to File on the menu bar, then select Exit, or press Ctrl-X.
?
2.3. Model Inputs
All model inputs must be specified by the user on the input page (Fig. 2.2.1). Inputs are grouped into three panels: General input (weather data, simulation mode, sowing or emergence date, maturity group, stem termination, plant population density, and early growth conditions); Water (optimum or rainfed, irrigation requirement estimation and irrigation inputs); and Soil (soil properties relevant for simulating soil moisture). The current version only simulates growth and yield without water limitation, and thus the rain fed and soil inputs are disabled. When selecting the single year simulation option, users can also provide a value of maximum LAI (based on the actual measurement or other information) to allow simulation of growth and yield based on the calibrated maximum LAI. The model provides default values of calibrated maximum LAI under different early growth conditions. Other calibrated options (maximum TDM and yield) are not yet enabled in the present version of the model.
?
2.4. Weather Data
When simulating yield potential (i.e. under optimal water regime) without estimating irrigation water requirements, the SoySim model requires three daily weather variables to run: total daily solar radiation (Solar), daily maximum temperature (Tmax), and minimum daily temperature (Tmin). When simulating growth under irrigated or optimal water regime with estimated irrigation water requirements, three additional daily weather variables are required: relative humidity (RH), precipitation (Rain), and reference evapotranspiration (ET).
All weather data must be stored in a plain text file (ASCII file) with the extension .wth. Below is an example of such a file for a site with daily weather data from January 1, 1990 to December 31, 2008:
CLAY CENTER(SC) NE Lat.(deg)= 40.57 Long.(deg)= 98.13 Elev.(m)= 552.
40.57 -98.13 552.00 -7.00 (lat long alt tz)
year doy Solar Tmax Tmin RH Rain ET
Mj/m2 deg C deg C % mm mm
1990 1 9.32 5.37 -15.70 66.2 0.00 2.39
1990 2 9.28 9.89 -7.71 66.8 0.00 2.41
1990 3 7.56 6.47 -7.35 77.2 0.00 1.78
1990 4 9.33 6.23 -8.15 62.1 0.00 2.06
1990 5 8.86 9.42 -11.00 65.3 0.00 2.06
...
...
2008 361 8.23 13.21 -3.59 83.1 0.00 2.13
2008 362 5.31 -0.10 -9.03 74.0 0.00 1.35
2008 363 8.61 7.30 -8.48 66.0 0.00 1.98
2008 364 8.61 7.85 -2.63 73.0 0.00 1.60
2008 365 8.63 7.45 -8.83 70.5 0.00 2.34
2008 366 8.51 -1.74 -13.19 73.9 0.00 1.40
?
?
It is important that all data are in the appropriate metric units, and are placed in a row in the order shown above. Detailed specifications for the weather file format are:
?
Row 1: Site information (location, latitude, longitude, elevation). All text in this row will be copied as site info to the output file of a simulation, but is not used in the simulation itself.
?
Row 2: Latitude (lat), longitude (long), elevation (alt), and time zone (tz) of the site. Latitude and longitude are in decimal degrees, while elevation is in m above sea level. The remaining part on this row is notation about the preceding inputs and should be left as it is. For the southern hemisphere, the latitude value must be negative. Similarly, longitude for the western hemisphere should have a negative value.
?
Row 3: Names of variables. Variables should be in the exact order shown. From left to right the variables are: year, doy (day of the year, 1-365 or 366 for leap year), solar radiation, Tmax (maximum temperature), Tmin (minimum temperature), RH (relative humidity), Rain (precipitation), and ET (reference ET).
?
Row 4: Measurement unit (metric) for each variable.Solar radiation = MJ/m2, temperature = oC, relative humidity = %, rainfall and ET = mm. If the data obtained are in other units, they must be converted to the appropriate metric units. If the data are in English units, daily solar radiation is often expressed in Langley (1 Langley=41.868 MJ m-2), temperature in oF (1 oF=(1 32)/1.8 oC), and rainfall and ET in inch (1 inch = 25.4 mm).
?
Row 5 to end: One row represents one day. Within a row, values must be separated from each other either by one or more spaces. Alignment is not important, and there is no limit to the number of decimals. If humidity, rainfall and ET are not available, the three variables must be entered as 0 (zero) and the model can only be used for simulating yield potential, without the water use and recommended irrigation simulations.
?
2.4.1. Sources of Weather Data
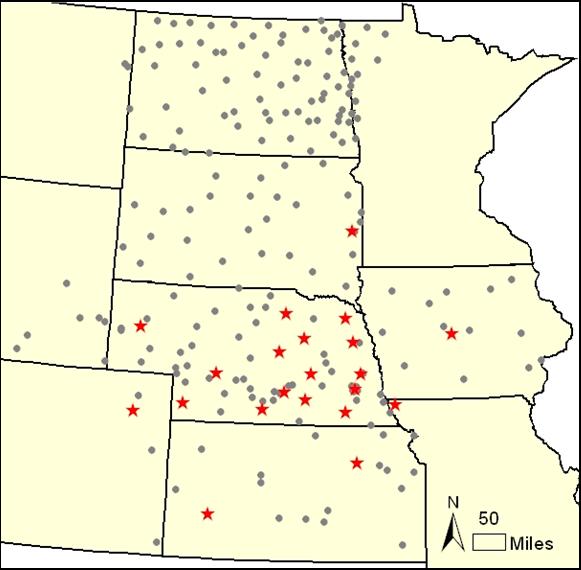
Figure 2.6. Sites of daily weather data included in the program package. The sites are part of the Automated Weather Data Network (AWDN) of the High Plains Regional Climate Center (HPRCC) of the University of Nebraska-Lincoln. The stars on the map show the locations of the sites included with your version of SoySim; the gray circles show other weather stations in the AWDN database. We recommend that users who wish to actively use SoySim to explore crop management options should purchase the complete AWDN database on CD-ROM from the HPRCC, or subscribe to specific sites, in order to obtain up-to-date weather data for locations in closest proximity to the sites for which simulations are desired.
?
The SoySim program package contains historical daily weather data obtained from the High Plains Regional Climate Center (HPRCC) for 21 selected locations in the western Corn-Soybean Belt. (Fig. 2.6, See the map and table below; data are provided until 12/2008.)
Table. 2.1. Sites of daily weather data included in the SoySim program package. The sites are part of the Automated Weather Data Network (AWDN) of the High Plains Regional Climate Center (HPRCC) of the University of Nebraska-Lincoln.
|
Site |
County |
State |
Latitude |
Longitude |
Elevation (m) |
Database period |
|
Alliance West |
Box Butte |
NE |
42o01' |
-103o08' |
1213 |
1/88-6/09 |
|
Beatrice |
Gage |
NE |
40o18' |
-96o56' |
376 |
1/90-6/09 |
|
Central City |
Merrick |
NE |
41o09' |
-97o58' |
517 |
1/86-6/09 |
|
Champion |
Chase |
NE |
40o24' |
-101o43' |
1029 |
1/82-6/09 |
|
Clay Center |
Clay |
NE |
40o34' |
-98o08' |
552 |
1/82-6/09 |
|
Concord |
Dixon |
NE |
42o23' |
-96o57' |
445 |
1/82-6/09 |
|
Elgin |
Antelope |
NE |
41o56' |
-98o11' |
619 |
1/88-6/09 |
|
Holdrege |
Phelps |
NE |
40o20' |
-99o22' |
707 |
1/88-6/09 |
|
Lincoln (IANR) |
Lancaster |
NE |
40o49' |
-96o35' |
357 |
1/86-6/09 |
|
Mead |
Saunders |
NE |
41o09' |
-96o29' |
366 |
1/82-6/09 |
|
North Platte |
Lincoln |
NE |
41o05' |
-100o46' |
861 |
1/82-6/09 |
|
ONeill |
Holt |
NE |
42o28' |
-98o45' |
625 |
1/85-6/09 |
|
Ord |
Valley |
NE |
41o37' |
-98o56' |
625 |
1/83-6/09 |
|
Shelton |
Buffalo |
NE |
40o44' |
-98o45' |
614 |
1/91-6/09 |
|
West Point |
Cuming |
NE |
41o51' |
-96o44' |
442 |
1/82-6/09 |
|
Akron |
Washington |
CO |
40o09' |
-103o09' |
1384 |
1/83-6/09 |
|
Ames |
Story |
IA |
42o01' |
-93o45' |
309 |
1/86-6/09 |
|
Brookings |
Brookings |
SD |
44o19' |
-96o46' |
500 |
1/83-6/09 |
|
Garden City |
Finney |
KS |
37o59' |
-100o49' |
866 |
1/85-6/09 |
|
Manhattan |
Riley |
KS |
39o12' |
-96o35' |
320 |
1/84-6/09 |
|
Rock Port |
Atchison |
MO |
40o28' |
-95o29' |
268 |
1/91-6/09 |
?
For more precise location-specific simulations, and particularly for real-time simulations in the current growing season (see sections 2.5.), users must acquire weather data directly from available public or commercial sources through free or fee-based subscriptions or by purchasing a downloadable data package. Many weather station networks in the US provide online access to weather databases, including daily historical records as well as daily records of the current growing seasons (Table 2.4.2)
?
Table. 2.2. Weather station networks in the USA that provide online access to weather databases
|
Center |
Website |
U.S. States |
|
National Climatic Data Center (NCDC) |
http://www.ncdc.noaa.gov |
All |
|
High Plains Regional Climate Center (HPRCC) |
http://www.hprcc.unl.edu |
NE, KS, IA, ND, SD, selected stations in other states |
|
Midwest Regional Climate Center (MRCC) |
http://mcc.sws.uiuc.edu |
MO, IA, MN, IL, WI, KY, IN, OH, MI |
|
Southeast Regional Climate Center (SERCC) |
http://water.dnr.state.sc.us/water/climate/sercc |
FL, SC, NC, GA, Al, MS, TN, VA, WV, MD, DE, KY |
|
Northeast Regional Climate Center (NRCC) |
http://www.nrcc.cornell.edu |
CT, DE, ME, MD, MA, NH, NJ, NY, PA, RI, VT, WV |
|
Western Regional Climate Center (WRCC) |
http://www.wrcc.sage.dri.edu |
AK, AZ, CA, CO, HI, ID, MT, NV, NM, OR, UT, WA, WY |
|
Southern Regional Climate Center (SRCC) |
http://www.srcc.lsu.edu |
AR, LA, OK, MS, TN, TX |
|
Illinois Climate Network |
http://www.sws.uiuc.edu/warm/datatype.asp |
IL |
?
Not all weather stations have complete weather data observations for long-term historical time periods, and spatial coverage varies. In particular, solar radiation data are often unavailable, except for more recent years and in the relatively new networks such as the AWDN at the HPRCC. Before subscribing or downloading data, check what data are available for a station located as close as possible to the location you wish to simulate, and make sure that solar radiation is included. For simulating long-term yield potential using SoySim, users should have access to a minimum of 10 years of historical weather data. Users should also check the format and measurement units of the daily data that are available, and how the data can be converted into the format shown above in section 2.4.
There will be cases in which some essential weather data are incomplete. SoySim will malfunction if a weather file contains missing data. In many cases, individual missing cells can be filled by extrapolating a value from surrounding dates. In some cases, long stretches of missing data in historical weather files might be filled in by averaging the same time period from years with complete data. For locations where no weather station with complete records is available nearby, various data sources could be combined to generate a more location-specific data set. Except for mountainous and coastal areas, solar radiation and temperature vary less than rainfall over short distances. Therefore, obtaining solar radiation and temperature from a weather station located within about 20-100 miles of your location is often sufficient for reasonable yield potential simulations. More precise rainfall and temperature data can be measured directly on-site by using relatively inexpensive rain gauges and a max/min thermometer, although both must be placed in an appropriate location.
?
2.4.2. Editing Weather Data
2.4.2.1 Manual editing of weather file: Once raw weather data have been obtained, they must be converted and formatted according to the specifications in section 2.4. This can be done most easily in spreadsheet programs such as Microsoft Excel. Once the units of the data are correctly entered and the data have been placed in the right columns with four rows of text on top, the file should be saved as a text file. After this, the extension of the weather file needs to be changed from .txt to .wth. Updating a weather file can also be done in a spreadsheet (e.g., Microsoft Excel) by opening the previously created .wth file and appending new data, then saving the file under the same name. Alternatively, .wth files can be edited in any text editor. New data, which must have correct units and order of variables, can then be appended as unformatted text to the end of the existing file.
NOTE: In text editors such as Microsoft Wordpad, one has to use Paste Special through the menu bar to select the unformatted text option for pasting when transferring text from Excel to a text file.
For example, a raw data file downloaded from a network such as AWDN may look like this:
CLAY CENTER(SC) NE Lat.(deg)= 40.57 Long.(deg)= 98.13 Elev.(m)= 552.
a257899 T-High T-Low Rel Hum Soil Tmp Wind Spd Solar Precip ET-NE
date/time F F % F@4 in. mi/hr langleys inches inches
1 1 1990 2400 41.675 3.740 66.227 26.157 9.504 222.334 0.000 0.094
1 2 1990 2400 49.802 18.122 66.832 28.580 8.499 221.403 0.000 0.095
1 3 1990 2400 43.637 18.770 77.206 30.036 11.903 180.338 0.000 0.070
1 4 1990 2400 43.216 17.330 62.107 30.025 8.377 222.789 0.000 0.081
1 5 1990 2400 48.956 12.200 65.264 28.435 6.472 211.358 0.000 0.081
Manual data preparation includes the following steps:
1.???? Conversion of all English units to metric (S.I.) units (solar radiation MJ/m2 = Langley/23.885; Temperature oC = 0.5556 x (oF - 32); rainfall and ET in mm = inch x 25.4.
2.???? Conversion of month-day format (first two columns) into running day format (day 1 = January 1 in each year, day 365 = December 31 in each year or 366 in a leap year),
3.???? Re-arrangement of data columns to arrive at the appropriate final file format:
?
CLAY CENTER(SC) NE Lat.(deg)= 40.57 Long.(deg)= 98.13 Elev.(m)= 552.
40.57 -98.13 552.00 -7.00 (lat long alt tz)
year doy Solar Tmax Tmin RH Rain ET
Mj/m2 deg C deg C % mm mm
1990 1 9.32 5.37 -15.70 66.2 0.00 2.39
1990 2 9.28 9.89 -7.71 66.8 0.00 2.41
1990 3 7.56 6.47 -7.35 77.2 0.00 1.78
1990 4 9.33 6.23 -8.15 62.1 0.00 2.06
1990 5 8.86 9.42 -11.00 65.3 0.00 2.06
?
4.???? Save the file as a tab delimited text file or MS-DOS text file (but not Unicode text file) with the extension .wth.
?
2.4.2.2 Downloading and conversion of weather data: Users in the High Plains region of the US can subscribe to the Automated Weather Data Network (AWDN) at the High Plains Regional Climate Center (HPRCC), University of Nebraska-Lincoln (http://www.hprcc.unl.edu). This data source has up-to-date online weather data for nearly 50 locations in Nebraska, as well as more than 100 locations in surrounding states. Data acquired from this source can be converted directly by the model from raw data to the units and format used by the Hybrid-Maize model. Follow these steps:
1.???? Log-on to the HPRCC Classic Online Service at:
 http://www.hprcc.unl.edu/services/index.php?p=online
http://www.hprcc.unl.edu/services/index.php?p=online
2.???? On the Web Data Access page, choose Select a Station from the list of choices shown in the upper left corner. Delete the current selection, then select a station from the list of available stations in the Automated Weather Data Network (AWDN) for your state. Add the highlighted station to the current list.
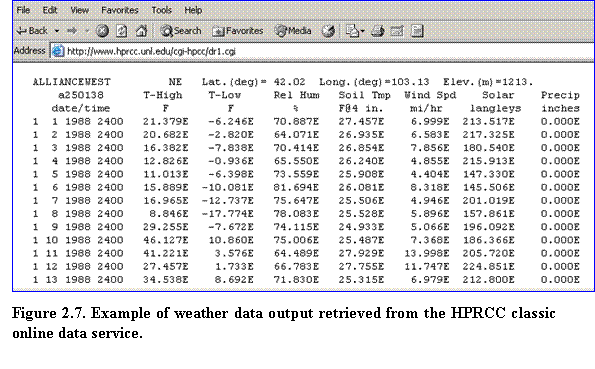
3.???? Click Raw Data Report from the list of choices shown in the upper left corner to enter the Data Retrieval page. Verify that the following options are selected: Time Frame: Begin and End Date; Output Format: Tabular; Units: English; and Sample Interval: Daily. Click on Click Here to Select These Options. Specify the start and end date, then click on Click Here to Submit Data Request. Weather data output will then be displayed on the web page based on the specified location and time interval (Fig. 2.7)
4.???? 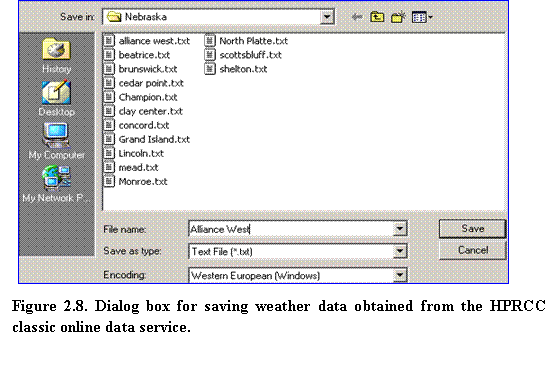 In your web browser, select File Save As and save the raw data file in the desired location. Make sure that Text File (*.txt) has been selected as file type. In the example shown in Fig. 2.8, this operation creates a raw data file named Alliance West.txt, stored in a Nebraska weather data folder.
In your web browser, select File Save As and save the raw data file in the desired location. Make sure that Text File (*.txt) has been selected as file type. In the example shown in Fig. 2.8, this operation creates a raw data file named Alliance West.txt, stored in a Nebraska weather data folder.
After saving the raw data in a text file, start the SoySim program. Click Tools on the menu bar and select Weather Utility (Fig.2.9).
?
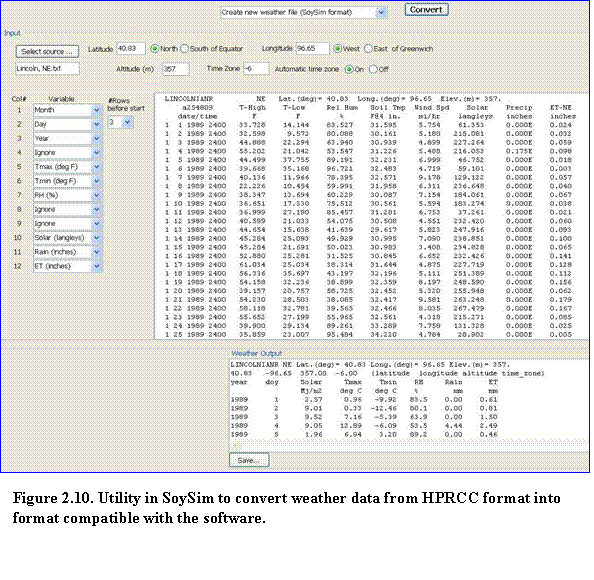
5.???? Click Select source and browse to the location in which the raw data file is stored and select it, then click OK. (Fig. 2.10). The weather data source will be shown on the upper text area. Enter the sites latitude, longitude, and elevation. Time zone can be set automatically (based on the longitude position of the site) or manually. Then click convert to convert the source weather data into a format usable for SoySim. Note that the convert button becomes enabled only if all the required inputs (latitude, longitude, elevation, and time zone) have been supplied. A message will appear to indicate once the conversion run is completed. Click OK to continue. The converted data (Weather data output) will be shown in the lower text area. Click the save button to save the formatted weather data to a file. Make sure the extension file of this formatted weather data as .wth.
?
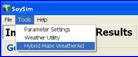
2.4.2.3 Importing weather data from the Hybrid-maize model: Hybrid-Maize users can take advantage of the option to import weather data from the Hybrid-Maize model using the Weather Utility tool included in the SoySim model. This import step is necessary considering the minor differences in the weather format between the two models. Weather file format in the SoySim model differs from that of Hybrid-Maize, as it contains additional site information, such as longitude and elevation, and does not allow more than eight columns of weather variables. To start importing weather data from the Hybrid-Maize model, select Import from hybrid maize model in the Select Task option (Fig. 2.11), then click the select source option.
?
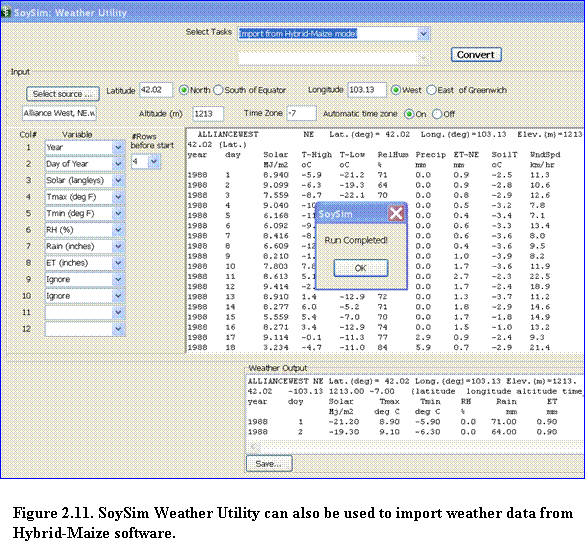
If Hybrid-Maize is installed in the default folder, (Program Files/Hybrid Maize) then the open file menu is directed to the Weather folder of the Hybrid-Maize program. Select the file to be imported by double clicking the file name or right clicking and selecting the open button. The content of the file to be imported will be shown in the weather source view area (upper text area). To complete the import, fill in the site latitude, longitude, and altitude (elevation) and then click the convert button (note that the convert button is enabled once all the necessary site inputs are supplied). Upon successful importing, a run completed message will appear. Click the OK button to continue, and the output of the weather importing will be shown in the Weather Output area. Save the imported file by clicking the Save button. By default, the save location is in the SoySim program directory, in the Weather folder(the file extension must be kept as .wth). The imported weather file is now ready to be used by the SoySim model.
?
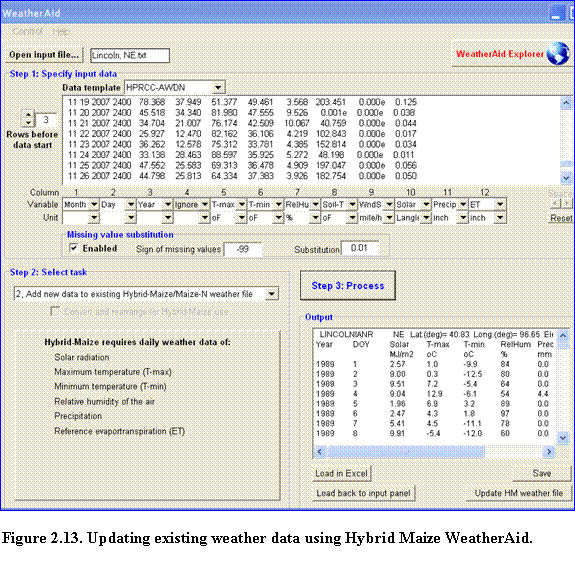
2.4.2.4 Updating SoySim weather data using Hybrid-maize WeatherAid: The Hybrid-Maize WeatherAid program can be used to update existing weather files for your SoySim software. Launch the program by selecting the Hybrid-maize WeatherAid under the SoySim Tools menu.
To update SoySim weather data using WeatherAid, make the new data (data to add to the existing set) available by clicking the open input file button, (if the new data are already available as text file in the drive) or by capturing the data online via WeatherAid explorer. Users with access to the HPRCC online data service can retrieve the online data by clicking the HPRCC online link. Follow steps 1 thru 3 in section 2.4.2.1. Upon completion of data request, take the following steps:
(1)? Click the Capture data button on the WeatherAid program (Fig. 2.12).
?
?
(2)? Select the appropriate data format (HPRCC-AWDN) and check the units of weather variables consistent with the data source.
(3)? Select Add new data to existing Hybrid-Maize/ MaizeN weather file in the select task menu.
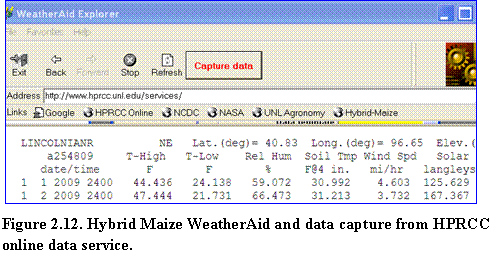
(4)? Step 3: Click the Process button (Fig.2.13).
Upon successful process, a menu will appear to allow selection of weather file to be updated. Select the weather file to be updated by double clicking on the name of the file or right clicking and selecting the open button. A pop-up message will appear to notify that the old file will be renamed with extension .wth.old. The updated weather file is now ready to be used for the SoySim model.
?
2.5. Simulation Modes
Single year: Simulation of growth in a single year (cropping season) is the default simulation mode. This mode is primarily used for analysis of past cropping seasons, in order to gain understanding of factors that may have caused yield loss, or to estimate the size of the exploitable yield gap by comparing simulated yield potential with actual measured yields. The year of simulation is selected from the drop-down box on the right, which lists all available years in the weather file.
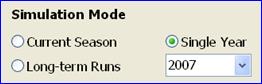
Long-term runs: This simulation mode is used for estimating the long-term yield potential at a given site, as affected by different choices of soybean maturity group ratings, sowing or emergence date, and plant population density. In other words, this mode can be used to explore how to exploit the available yield potential through management.
In this mode the model simulates maize growth in each year of a range of years with available weather data. All runs (=years) are ranked based on grain yield, and simulated values are only shown for the years with the maximum (best), 75% percentile, median (50% percentile), 25% percentile, and the minimum (worst) yield. The summary results table also displays the numerical mean calculated from all simulations of all years. It is important to remember that all runs (years) in this mode will display grain yields and other simulated data with respect to the same set of input data (e.g. planting or emergence date, MG, etc).
?
Current season: This mode is used for in-season (or real-time) simulation of soybean growth and forecasting the final yield before the crop matures. Predictions are based on up-to-date weather data for the current growing season, supplemented by historical weather data for the rest of the season at the simulation location. To use this mode, the weather data file must contain at least ten years of reliable weather data for the site, in addition to updated real-time weather data for the current growing season.
When this mode is selected, the year selection box will be grayed out and the last year (i.e. the current year) of the weather file will be selected automatically as the year for which a prediction is to be made. For locations at which a growing season crosses into another year (such as in the southern hemisphere where crops are planted in September/October and harvested in the following year,) the year in which the current season starts will automatically be selected. Note that this mode will not run properly if the weather data for the current season are already available for the entire growing season.
In the current-season mode, the model first uses the current years weather data to simulate actual growth up to the current date with available actual weather data, and then utilizes the climate data for each subsequent day based on historical weather data from all previous years, in order to simulate all possible growth scenarios until crop maturity. Predictions are ranked according to grain yields and results are shown for the scenarios with the best, median (i.e. 50% percentile), and the worst yields.
In the current season mode, the model provides detailed graphs related to growth, water use, and weather parameters during the growing season, but only for the best yield scenario.
?
2.6. Crop Management Inputs
Start from: A SoySim simulation can start from either sowing or emergence. Make that choice and select the appropriate date from the month/date boxes on the right. When starting from sowing, the sowing depth needs to be specified, because the depth of seed placement affects the time required for emergence, as simulated by the model (the seed depth text box will appear once the user selects starting date from sowing). If available, use date of emergence for the start of simulation, because that date can be easily observed in the field and provides more accurate simulations. To view a description of emergence for soybean, double click the Emergence button.
?
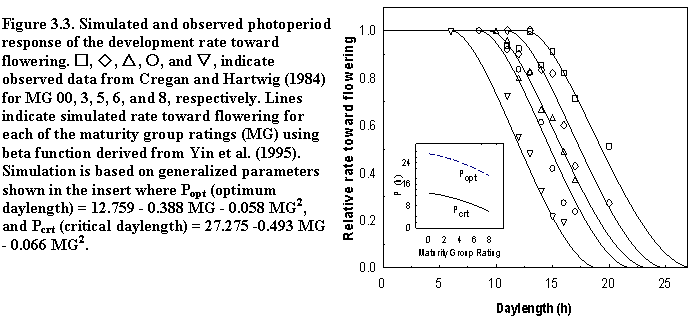
Cultivar: This sub-panel is used to specify genotype-specific phenology and growth characteristics. The current version provides a generic option of genotypic parameterization, in that the users only need to supply the relative maturity group rating and stem termination type. The alternative option of directly modifying genotypic parameters is currently disabled. For comparing genotype within the same maturity group, the latter option may be useful, but at the moment, the model assumes the best-adapted cultivar (for the given maturity group and stem termination type) is being used for the given site. Maturity group rating and stem termination type are used in SoySim model for characterization of plant developmental response to temperature and daylength (Setiyono et al., 2007), while stem termination type determines the relationship between plant population density and maximum plant leaf area (Setiyono et al., 2008).
?
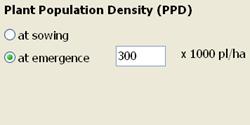
Plant population: Enter the plant population density (PPD) at emergence or sowing, in 1000 plants per acre (English) or 1000 plants per ha (metric). Plant population density at sowing is the same as the number of viable seeds sown per acre or ha. If the user selects PPD at sowing, a pop-up message appears to give a suggestion of what percent emergence to use under optimum conditions. The acceptable value of plant population density that the user can enter ranges from 186 617 thousands plants/ha (75.3 to 250 thousands plants/A). A popup error message will appear if the user tries to enter a value of PPD outside this range.
|
|
|
|
NOTE: The SoySim model has mostly been tested with plant population densities ranging from approximately 186,000 to 617,000 plants/ha (75,300 to 250,000 plants/A). The model should be used with caution outside this range. Actual crop response to plant population may also vary significantly among cultivars. Effects of different row spacing are not accounted for in SoySim model. |
|
2.7. Water
This version of the SoySim model only simulates yield under non-water limiting conditions. Therefore, the optimum option in the water section is always enabled, while the rainfed/ irrigated option is disabled and grayed out.
Optimum: This option is selected for simulating soybean growth under non-limiting conditions, assuming adequate water supply throughout the entire growing season (see section 1). When selecting Optimum water regime, the user also has the option to let the model estimate the minimum requirement for irrigation water in order to achieve non-water limiting growth. Only the crop evapotranspiration (ET) approach is available in this version of SoySim. The soil water balance approach may be available in a future version. Unlike the soil water balance approach, the crop ET approach did not require soil properties and rooting depth inputs, therefore the soil and rooting depth inputs section is grayed out in this version.
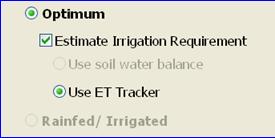
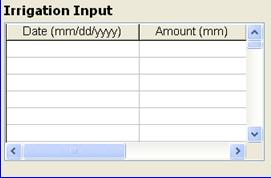
With the single year or the in-season simulation mode, estimation of irrigation requirements under the optimum water option can be combined with user-provided irrigation events. In this case, the user can enter the actual or hypothetical dates and amounts of irrigation applied for the soybean crops in the field in the Irrigation Input table. The estimation of irrigation requirements takes into account these actual irrigation events and estimates the remaining irrigation amount needed to satisfy the soybean water use as estimated by the crop evapotranspiration rates. To replace recommended irrigation with the actual event, enter the at least one day prior to the recommended date. Entering the same date as the recommended will not replace the recommended irrigation
?
2.8. Model Outputs
Once a simulation run has been completed, the screen display will move from the Input page to the Result page. The simulation run is faster with the single year mode, as compared to the long-term and current-season mode, as the latter modes requires the model to simulate growth in multiple years. The Result page consists of the Text and Graph sub-section. With the long-term or current-season simulation mode, the Result page has an additional tab, Comparison.
?
2.8.1. Text Results
?
The text display of the simulation results differs depending on the mode of simulation. In single year and current-season modes, the text-results are shown on one page (use the scroll bar to view the lower part). In long-term simulation modes, the text-results display can be toggled between across years (Summary) or by Individual Year, by clicking the appropriate radio button.
?
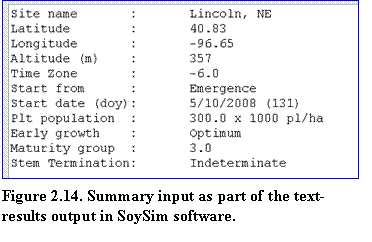
In any simulation modes, the display of the text-results page begins with a summary of the input that includes key weather station site information (name, latitude, longitude, elevation, and time-zone,) and agronomic management (start from, start date, plant population density, maturity group, and stem termination) (Fig. 2.14).
Also listed in this input summary is the user selection of early growth conditions (optimum, medium, or poor). At any timeregardless of the units selected in the input pagethe units in the text-results page can be changed between Metric and English by clicking the unit option button at the top right corner of the page.

?
Single-year run: The results consist of phenology, summary and details of daily growth variables. Key predicted dates of vegetative and reproductive stages are listed in the phenology section (Fig. 2.15).
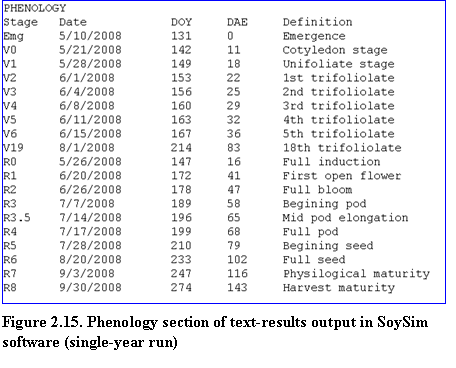
?
Scrolling down this page discloses the summary of the simulated growth variables, including yield and dry matter accumulation at physiological (R7) and harvest (R8) maturity, harvest index, and maximum LAI (Fig. 2.16).
?

?
Next, the text-result page provides growth and related variables in daily intervals beginning from emergence to harvest maturity (Fig. 2.17).
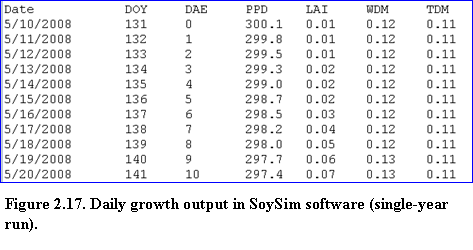
?
Variables definitions, including the ones listed in the phenology and growth sections, are listed at the bottom of the text-result page. The last section of the text-result page under single-year simulation mode lists the recommended irrigation events for optimum (non-water limiting) yield.
?
Long-term Runs: These results consist of two pages: (1) across-year summary of growth simulations (Fig. 2.18), and (2) individual year growth simulation. The across-year summary growth page lists the simulated yield, biomass accumulation, harvest index, and maximum LAI in all of the simulation years with available weather data. The remark column notes which years had the best, median, and worst yields. Mean yield from this long-term run is also given at the bottom of the list.
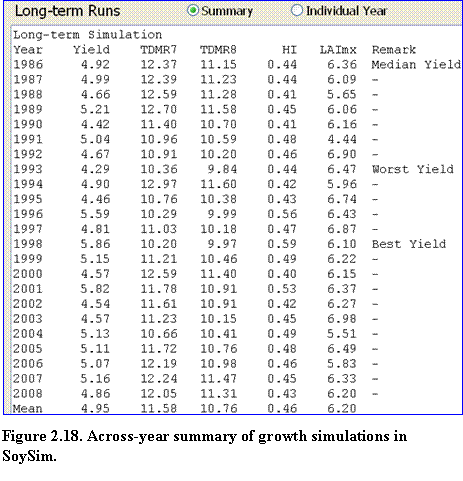
?
The user can toggle the results page to see the details of daily growth output of this long-term simulation, by clicking the Individual Year button (Fig. 2.19). The daily output consists of total above ground dry matter, seed dry matter, and LAI.
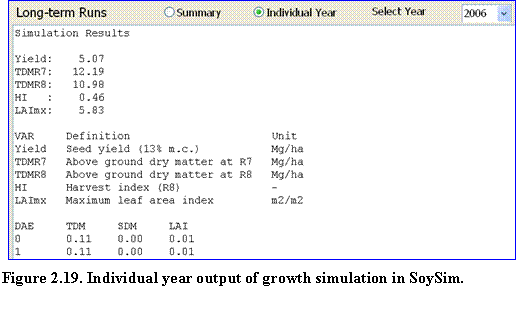
?
?
Current season run: These results consist of phenology, summary and details of daily growth variables. Key predicted dates of vegetative and reproductive stages are listed in the phenology section, along with additional columns of earliest and latest occurrence of the phenological stages (Fig. 2.20).
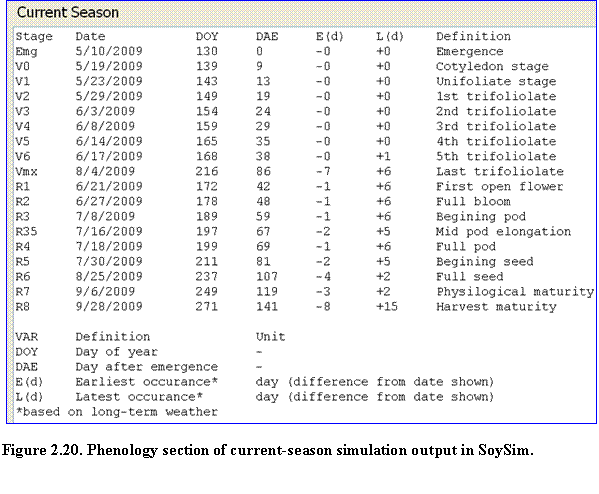
Such ranges in predicted dates are due to the use of historical weather data; the model evaluates the earliest and latest occurrence given the temperature and day length conditions in the past years for days beyond the available actual weather data in the current year. Notice that for the phenological stages that occurred during the actual weather data (past days), there is no range of predictions. The model simulates the stage based on the current year weather data. Only for phenology stages that occurred at future dates (dates without actual weather data) will the model provide ranges of predictions.
The summary growth section lists the yield, biomass, harvest index, and LAI for several statistical yield ranks (best, 75th percentile. median, 25th percentile, and worst) and the mean yield of the current season simulation (Fig. 2.21).
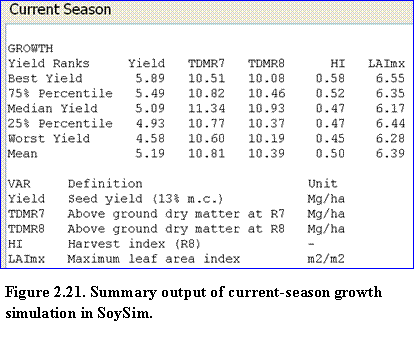
The user can scroll down further to observe the daily output details of total above ground and seed dry matter, and LAI for the best, median, and worst yield scenarios.
2.8.2. Graphs
This page of the results provides graphs of growth variables during the growing season. The user can switch the units between the Metric and English systems, regardless of the unit selected on the input page. Likewise, the category of horizontal axis in the graph can be switched between day after emergence (DAE) and calendar date.
Long-term Runs: The user can select graphs of growth for each year of the available weather data by selecting a year in the Select Year list (Fig. 2.22). 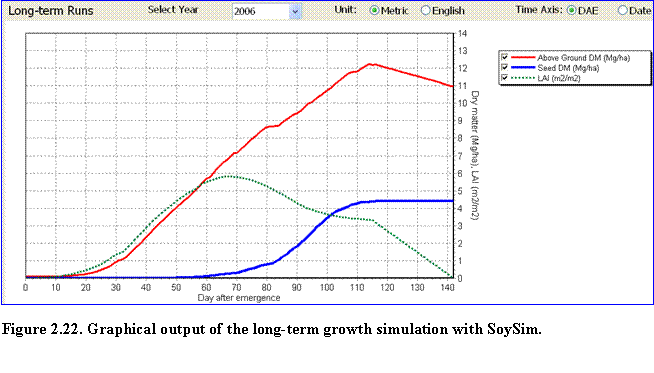
The graph displays total above ground (TDM), LAI, and seed dry matter (SDM) distribution during the growing season for a given year in the long-term simulation.
?
Single Year Run: There are additional variables in the graph when the user runs the simulation with the single year run mode. The graph contents are divided into four options: (1) Growth & Assim. & Resp. Rates; (2) Growth & Water Use; (3) Growth and Weather; and (4) Water Use and Weather. The Growth & Assim. & Resp. Rates option allows the user to observe growth variables in conjunction with assimilation and respiration rate variables (Fig. 2.23).
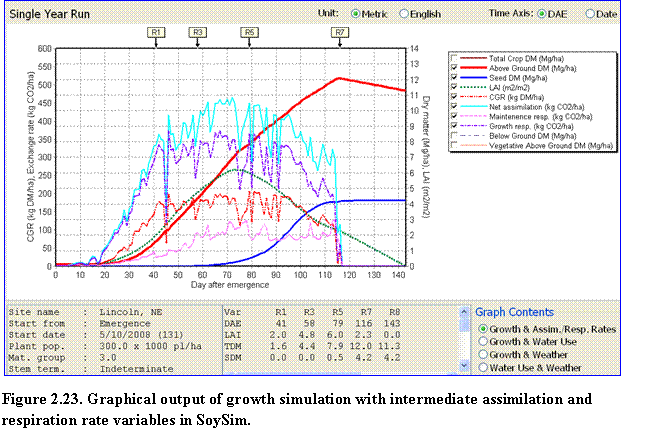
Similarly, the other options provide a mean to compare various variables of a given categories, such as growth versus water use, growth vs. weather, and so on. Graph Contents buttons are located in the lower right corner of the Graph page.
The box in the lower left corner of the graph page lists the summary of user inputs for the given simulation, while the box in the lower middle section lists the occurrences of key R-stages, along with the mean values of certain key variables between these stages. The variables listed in this box change depending on the Graph Contents being selected.
?
Current Season Run: With the current season simulation mode, the user can view either the Summary or Details of the growing season graph. The Summary graph displays the dynamic total above ground (TDM) and seed dry matter (SDM) distribution during the growing season. The bold part of the TDM curve represents the simulation of biomass accumulation based on the actual weather data that ends at the date of last available current year weather data (Fig. 2.24). Thereafter, best, median and worst-yield simulation scenarios are displayed. Such simulation scenarios are also displayed for the seed dry matter.
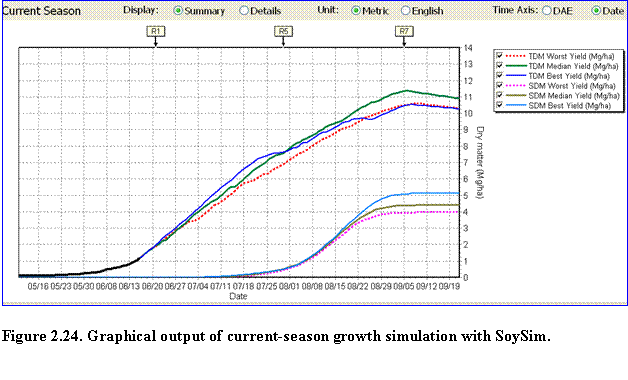
?
The Details option of the growing season graph is similar to the single-year run mode, in that there are four categories of graph contents to display (Fig. 2.25).
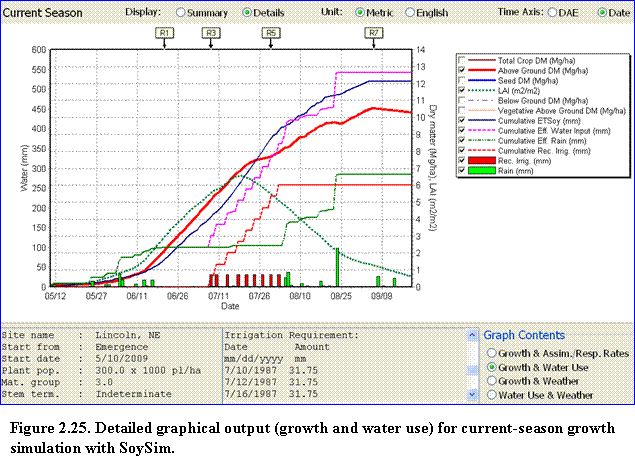
In this case, the simulation is for the best-yield scenario. As with the single-year run, the lower middle box displays the occurrences of key R-stages and values of the graph variables between the given stages. Scrolling down further in this box, the user can view the values and dates of irrigation requirement for the best-yield scenario.
?
2.8.3. Comparison
This page is only available under the long-term and current season simulation modes. The page displays bar charts to compare yield, total above ground dry matter (TDM), and harvest index for all of the years included in the long-term simulation.
It also compares these variables for the different statistical ranks of yield (best, 75th percentile, median, 25th percentile, and worst-yield) for the long-term simulation or the current season simulation mode (Fig. 2.26).
?
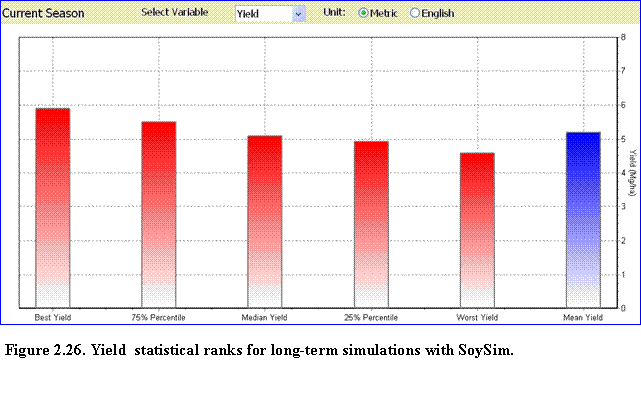
?
?
2.9. Weather
This page displays a graph of weather variables for a given weather station. To view the graph, the user doesnt have to run the simulation. Once a weather data is selected by clicking the weather file button on the input page, the graph of weather variable of the given weather station is available and can be viewed by clicking the weather page tab.
The weather graph page has simple graph control components in the lower left and middle sections of the graph (Fig. 2.27).
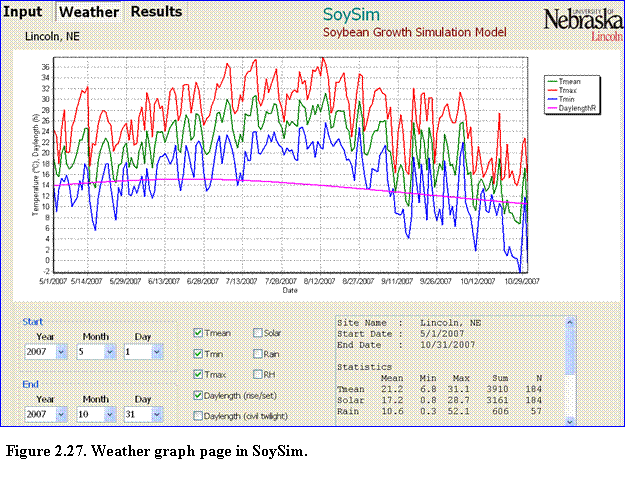
The first graph control component is the starting and ending date, which define the range of the weather variables displayed on the graph. The starting date must be earlier than the ending date. The ending date cannot be beyond the date of the available weather data. The box in the lower right-hand corner of the weather graph page displays the statistical summary (mean, minimum, maximum, sum, and number of data) of weather variables within the specified range. Note that the summary calculation only considers the first 365 days if user enter a range that exceeds 365 days.
?
3. Detailed Information about the SoySim Model
Crop simulation models are mathematical representations of plant growth processes as influenced by interactions among genotype, environment, and crop management. They have become an indispensable tool for supporting scientific research, crop management, and policy analysis (Fischer et al., 2000; Hammer et al., 2002; Hansen, 2002). Simulation models serve different purposes, and the intended purpose influences the level of detail needed for mechanistic description of key processes, sensitivity to environment and management, data requirements, and model outputs. All cereal and legume crop models must simulate plant growth and development, biomass partitioning among organs (leaves, stem, root, and reproductive structures), and yield formation. The accuracy of simulating the outcome of these processes across a wide range of environments depends on basic understanding of the key ecophysiological processes and incorporating this knowledge in the mathematical formulations that constitute the model.
Our objective was to develop a model that can provide robust simulation of soybean yield potential in different environments with a minimum number of location- or cultivar-specific input parameters. Agronomists need such robust crop models to improve the efficiency of research that investigates interactions among crop management options in favorable environments, while crop producers and crop consultants need such models for use in computer-based decision-support tools to improve crop management decisions.
The SoySim model combines existing approaches for photosynthesis simulation (Farquhar type framework) and biomass accumulation and partitioning (similar to the WOFOST model) with several new components: simulation of flowering based on floral induction and post-induction processes (Setiyono et al., 2007), leaf area index simulation with a logistic function (Setiyono et al., 2008), integration of canopy assimilation using a beta function, and yield simulation based on assimilate- and phenology-driven seed number and individual seed growth. SoySim model simulates soybean growth on daily basis from emergence to harvest maturity. The model is potentially more responsive to changes in environmental conditions than models such as CROPGRO-Soybean and Sinclair-Soybean, and WOFOST. The SoySim model also requires fewer genotype-specific parameters without sacrificing prediction accuracy.
Detailed descriptions of major model components are provided in the following sections.
?
?
3.1. Phenology
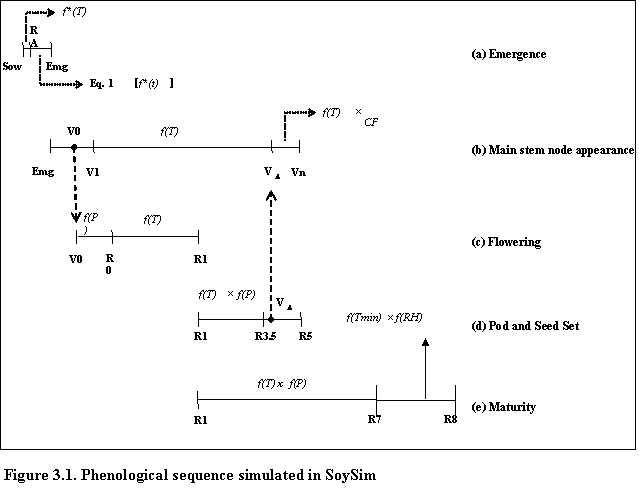
SoySim simulates soybean phenology based on five main phases (Fig. 3.1). The V- and R- stages terminology are based on Fehr and Caviness (1977).
The first phase, from sowing to emergence, is based on accumulated thermal time during radicle development (sowing radicle appearance, RA) and hypocotyl elongation (RA emergence).
The next main phase is from emergence to final main stem node (Vn) and is a function of temperature and a chronology function describing reduction of main stem node appearance rate. Since soybean development is not sequential, as in cereals, the beginning of reproductive phase overlaps with continuing vegetative phase. Therefore, the next main phase, which ends at the first open flower (R1), commences at the cotyledon stage (V0), and is a function of photoperiod during the floral induction phase (V0 R0) and temperature during the post-induction phase (R0 R1).
The subsequent main phase, which ends at beginning seed (R5) is a function of temperature and photoperiod. Just prior to R5, the chronology function is applied to decrease main stem node appearance in the vegetative phase. The onset of reduction in main stem node appearance rate (VD) is simulated based on mid-phase R1-VD.
The maturity main phase (R1-R8) is a function of temperature and photoperiod from the flowering to physiological maturity (R1-R7) and a function of minimum temperature and relative humidity from physiological maturity to harvest maturity (R7-R8).
Emergence is simulated in SoySim using a similar approach as in the STICS model (Brisson et al., 2003), where the radicle appearance (RA) and hypocotyl elongation are simulated sequentially. Radicle appearance is simulated when the accumulated thermal time (base temperature of 5C) is at 40C days. Afterwards, hypocotyl length (HL) is calculated using the accumulated thermal time from radicle appearance until emergence:
where a, and b are constants, Hmax is maximum hypocotyl length (cm), and ATTra is accumulated thermal time since radicle appearance (Cd). The values of a, b, Hmax, and base temperature (Tb) used in SoySim are 0.0128, 4.57, 5 cm, and 5C, respectively. The value of a was derived from observed data in Lincoln, NE in 2004, while b, Hmax, and Tb are parameters given for soybean in STICS (Brisson et al., 2003). Emergence is defined as when the hypocotyl length exceeds sowing depth plus 0.6 cm. This latter value (0.6 cm) was added to ensure that emergence represents the cotyledon being above the soil surface.
Accumulated values of the daily developmental rate are used to determine the occurrence of unifoliate (V1), floral induced (R0), first open flower (R1), beginning seed (R5), and physiological maturity (R7). The daily development rate (r) is calculated with the following relationship:
where Rmax is maximum development rate (d-1) at optimum temperature and photoperiod, f(T) is temperature function, and f(P) is photoperiod function. For developmental phases that are not sensitive to temperature or photoperiod, the temperature or photoperiod function, respectively, equaled one.
The temperature response, f(T), in SoySim is based on a non-linear beta function (Fig. 3.2), the version used in Wang and Engel (1998) with appropriate cardinal temperatures for each phase as shown in Table 3.1:
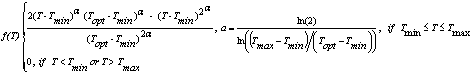 (3)
(3)
?

where, for a given phase, Tmax is temperature above which the development rate is zero (C), Tmin is temperature below which the development rate is zero (C), Topt is temperature at which the development rate is optimal (C), a is beta function shape factor, T is mean daily temperature (C).
?
Table 3.1. Generic (non-cultivar specific) parameters for phenology simulation in SoySim
|
Phase |
Tmin |
Topt |
Tmax |
Pcrt |
Popt |
B |
Rmax |
|
? |
----------------C----------------- |
---------h-------- |
d-1 |
||||
|
EmergenceV1 |
5.0A |
31.5A |
45.0 A |
0.1194E |
|||
|
EmergenceV0* |
5.0A |
31.5A |
45.0 A |
0.1990E |
|||
|
V1Vn |
7.6E |
31.0A |
40.0E |
0.4520E |
|||
|
V0R0 |
11C |
25C |
-6.00 |
0.2500D |
|||
|
R0R1 |
7.0A |
32.4A |
41.9 A |
0.0738E |
|||
|
R1 R5 |
3.6E |
25.0B |
40.0E |
12E |
18E |
-0.83 |
0.0483E |
|
R1 R3.5* |
3.6E |
25.0B |
40.0E |
12E |
18E |
-0.83 |
0.0790E |
|
R1VD* |
3.6E |
25.0B |
40.0E |
12E |
18E |
-0.83 |
0.0690E |
|
R1R7 |
0.0E |
21.5E |
38.7E |
12E |
18E |
-0.83 |
0.0168E |
?
*Mid-phase is simulated using mid-phase coefficients (0.60 for EmergenceV0, 0.613 for R1R3.5, 0.704 for R1VD). Cardinal temperatures and daylengths for a mid-phase are the same as the corresponding main or sub-phase. Rmax for a mid-phase equaled to Rmax of the corresponding main or sub-phase divided by the mid-phase coefficient. V1 is unifoliate stage, V0 is cotyledon stage, Vn is end of main stem node appearance, R0 is end of floral induction, R1 is first open flower, R5 is beginning seed, VDis beginning of the reduction in main stem node appearance rate, R7 is physiological maturity. Tmax is temperature above which the development rate is zero (C), Tmin is temperature below which the development rate is zero (C), Topt is temperature at which the development rate is optimal (C), Pcrt is photoperiod above which development rate is zero (h), Popt is photoperiod below which development rate is optimal (h), B is solar elevation angle (). Letters after the parameters values indicate the source of estimation: (A) Hesketh et al. (1973), (B) Brown and Chapman (1960), (C) Cregan and Hartwig (1984), (D) Taiz and Zeiger (1991), (E) Field Data (Lincoln, NE, 2004).
The photoperiod response in SoySim is based on a non-linear beta function, modified from the version described in Yin et al. (1995) with the cardinal daylength for each phase as shown in Table 1 (Fig. 3.3):
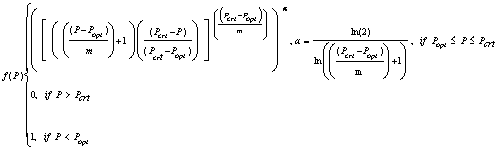 (4)
(4)
?
where, for a given phase, Pcrt is daylength above which development rate is zero (h), Popt is daylength below which development rate is optimum (h), P is daylength (based on -6.00 and -0.83 solar elevation angle for floral induction and post-flowering photoperiod responses, respectively), m is constant (3.0 h).
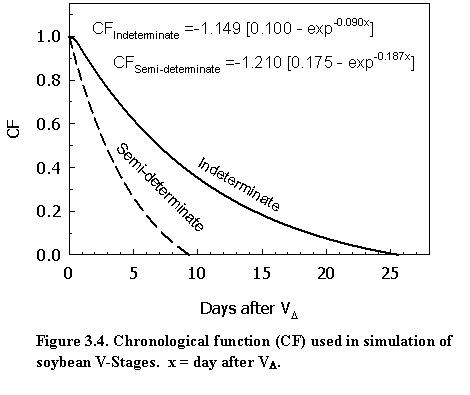
Main stem node appearance rate (rNA) after unifoliate stage is accumulated to simulate the subsequent V-stages and is calculated by the following equation:
![]() (5)
(5)
![]() (6)
(6)
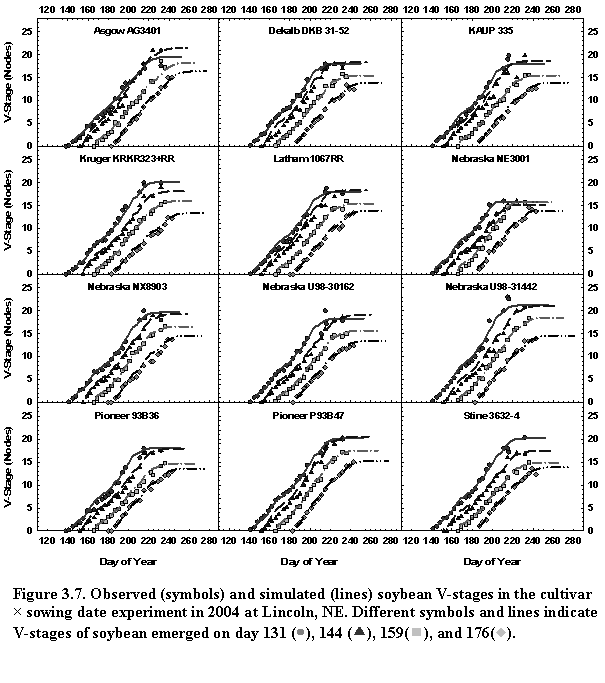
where rNA is main stem node appearance rate (node d-1), rNA,max is maximum main stem node appearance rate (node d-1), CF is chronological function for reduction of main stem node appearance rate, x is days after VD (the onset of reduction in main stem node appearance rate), and A, B, C are chronology function coefficients. The values of chronology coefficients A, B, and C for indeterminate and semi-determinate cultivars are 1.149, 0.1, 0.09, and 1.210, 0.175, 0.187, respectively. These chronology coefficients were derived from node appearance data of NE3001 (semi-determinate, MG 3.0) and Pioneer P93M11 (indeterminate, MG 3.1) in the 2005 growing season in Lincoln, NE. Daily main stem node appearance rate is first estimated by plotting V-stage data on day of year. The day when the estimated node appearance rate is reduced from its optimal value is noted as VD. CF is calculated as ratio of the current day main stem node appearance rate and the optimal node appearance rate. VD is associated with the reproductive phase R1-R5 (Fig. 3.4).
?
?
3.2. Leaf Area Dynamics
Leaf area index is simulated as a function of net leaf area and population density. The term net leaf area is used to account for the simultaneous occurrence of leaf expansion and senescence at the whole plant and population level.
![]() (7)
(7)
where LAI is leaf area index (m2 m-2), Lnet is net leaf area (cm2 plant-1), PD is population density (plants m-2) and 104 is a conversion factor from cm2 to m2.
Population density in Eq. 7 is allowed to change linearly from V2 stage to physiological maturity (R7) to account for post-emergence attrition (Eq. 8). The reduction in plants population is a function of initial population density (at V2 stage), based on field observations in 2004 and 2006 in Lincoln, NE (Eq. 9).
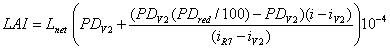 (8)
(8)
![]() (9)
(9)
?
where PDV2 is population density at V2 (plants m-2), PDred is the amount of reduction in population density due to post-emergence attrition (%), i is current days after emergence, iV2 is days after emergence at V2, and iR7 is days after emergence at R7.
Net leaf area is the difference between gross accumulated and senesced leaf area (Eq. 10). Gross accumulated and senesced leaf area are determined based on current day rates of change and the previous values of these variables (Eq. 11 and 12).
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
where Lg is cumulative gross leaf area (cm2 plant-1), Ls is cumulative senesced leaf area (cm2 plant-1), Lgi-1 and Lsi-1 are previous day Lg and Ls, respectively. dLg is rate of change in Lg(cm2 plant-1), dxg and dxs is rates of change in cumulative f(T) for the expansion phase and senescence phases, respectively, where f(T) is a temperature function (Eq. 10), and di is the time step (d).
?
The rate of change in gross leaf area is simulated using the first derivative of a logistic function (Eq. 7) and accounting for the effect of air temperature (Eq. 16). The logistic function used has the form of Lg = ag/[1-bg exp(-cgxg)], where ag is the Lg-asymptote, bg is a shape factor, and cg is a rate constant (Milthorpe and Moorby, 1979). The variable bg is related to ag and the intercept of Lg at xg=0 (Eq. 14), while cg is related to ag and the slope of Lg at the inflection point (Eq. 15) (Milthorpe and Moorby, 1979). In the model, not the actual intercept of Lg at xg=0, but rather a pseudo initial value (Lg) is used in determining bg. Lg influenced the initial rate of change in Lg. This assumption is considered because the immediate variable of interest is the rate rather than the state value of Lgand the nature of the logistic curve does not allow a reasonable value of Lgat xg = 0. The true initial Lg (Lgo) is given as an input parameter (Eq. 11).
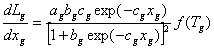 (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
?
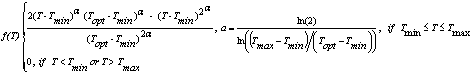 (16)
(16)
?
where dLg/dxg is the rate of change in gross leaf area per change in cumulative f(T) (cm2 plant-1), ag is the maximum gross leaf area (cm2 plant-1), Lg is a variable influencing the initial rate of change in Lg (cm2 plant-1), dLgIP is the rate of change in gross leaf area (cm2 plant-1) at its peak, xg is the cumulative f(T) since emergence with minimum (Tmin), optimum(Topt), and maximum (Tmax) temperatures of 0,33, and 50 C, respectively, f(T) is the temperature response function of leaf expansion (Eq. 16).
The reason for using the derivative rather than the logistic function itself in simulating Lg is because the fluctuations of temperature and water availability directly alter the rate rather than the state variable of Lg. The logistic function is used with the assumption that accumulative Lg is characterized by three distinct phases. Lg increased exponentially due to the rapid vegetative growth during the first phase. In the second phase, Lgincreased at nearly a constant rate as leaf appearance and expansion proceeded at a steady state. The final phase described a diminishing rate of Lg as no more leaves were produced at the end of node appearance.
A beta function (Wang and Engel, 1998) and data from the literature is used to describe temperature response of soybean leaf expansion f(Tg). A different set of cardinal temperatures are used than that of temperature response for xg. Temperature response for xg described the developmental factor of potential leaf expansion while f(Tg) emphasized the sensitivity of the potential rate of leaf expansion to temperature fluctuation.
Field experiment data from Lincoln, NE in 2004 and 2005 and literature data were used to generate the function relating population density and the maximum leaf area and the influence of air temperature on the parameters governing the logistic equation for leaf expansion.
The senesced leaf area index (LAIs) is simulated as a function of expanded leaf area (LAIg) and a variable determining the fraction of senesced leaf area (Lsf). Lsf is determined based on the average solar radiation from emergence to initialization of senescence and a function of plant population density.
LAIs = LAIg Lsf (17)
Lsf = (-0.0771 RsLs + 2.2802) f(PD) (18)
f(PD) = (-0.0105 PD) + 1.2943 (19)
where RsLsis average solar radiation from emergence to initialization of senescence, and f(PD) is function of plant population density, and PD is population density (plants m-2). The above algorithm is based on the hypothesis that solar radiation environment is negatively correlated with the fraction of senesced leaf area. Soybean plants growing under higher solar radiation intensity are likely to have more gradual leaves senescence as compared to those under lower solar radiation intensity. Likewise, high population densities promote more gradual leaf senescence as compared to lower population densities. Such hypotheses are supported by the empirical observation in field experiment in Lincoln, NE in 2004 and 2005. The variable Lsinit determines the day of senescence initialization which occurred at a defined progress toward R1 stage. In SoySim model, the gradual leaf senescence is followed by a rapid senescence between the R7 and R8 stages. The senescence between these stages is simulated based on a linear function allowing the leaf area to reach zero by the R8 stage.
?
3.3. Dry matter accumulation and partitioning
Whole crop biomass (WDM), aboveground dry matter (ADM), and root dry matter (RDM) in kg ha-1 are simulated using the framework of Supit and Van der Groot (2003):
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
where WGR is whole crop growth rate (kg ha-1 d-1), t is time interval in days, pRDM is the partitioning coefficient to root dry matter (kg kg-1), and the subscribe i-1 indicates the crop biomass (kg ha-1) on the previous day. The partitioning coefficient for root (pRDM) was derived from published data.
WGR is estimated on a whole crop basis by gross assimilation and maintenance respiration following Supit and Van der Groot (2003):
![]() (23)
(23)
where Yg is a conversion efficiency factor for assimilate (kg kg-1), A is the gross assimilation rate
(kg ha-1 d-1), and Rm is maintenance respiration rate (kg ha-1 d-1). Yg is defined as:
![]() (24)
(24)
where YADMand YRDMare conversion efficiency factors for assimilate to ADM and RDM,
respectively (kg kg-1), which were estimated using values from WOFOST and the calibration
dataset. Eq. 24 is a simplified version of the function described in Supit and Van der Groot (2003) in that eq. 24 does not account for biomass partitioning among structures such as stems, leaves, and storage organs. Rm is sensitive to temperature as follows:
?
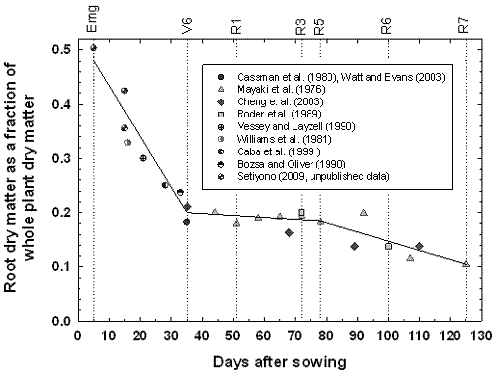
Figure 3.5. Soybean root dry matter fraction of whole plant dry matter during the growing season based on Setiyono (2009, unpublished data, field experiment) and published data from experiments conducted in the field (Mayaki et al., 1976; Roder et al., 1989), greenhouse (Bozsa and Oliver, 1990; Cassman et al., 1980; Cheng et al., 2003; Watt and Evans, 2003), and growth chamber (Caba et al., 1999; Vessey and Layzell, 1990; Williams et al., 1981). Developmental stages (Fehr and Caviness, 1977) are shown on top of the graph. The solid line indicates the dry matter fraction values used in SoySim.
?
![]() (25)
(25)
?
where Rmr is maintenance respiration (kg ha-1 d-1) at a reference temperature (Tr) of 25 C, Q10 is fractional increase or decrease in respiration rate per 10 C change in temperature, and T is hourly temperature (C). Rmr is simulated as function of biomass and maintenance respiration coefficients for TDM and RDM:
![]() (26)
(26)
where rADM and rRDM are maintenance respiration coefficients (kg kg-1 d-1) for ADM and RDM, respectively.
Photosynthesis converts 6 moles of CO2 into one mole of carbohydrate:
![]() (27)
(27)
thus biomass assimilation rate is calculated based on the carbon exchange rate as:
![]() (28)
(28)
where Pnis daily canopy photosynthesis rate (kg CO2 ha-1 d-1) and the term 180/264 represents
the molecular weight ratio of one mole of carbohydrate to six moles of CO2. The conversion term is commonly simplified to 30/44 kg carbohydrate kg-1 CO2.
Pn is calculated by integrating the hourly canopy photosynthesis (Pc) rate over the day. Pc is simulated by the integration of individual leaf photosynthesis rates over the whole canopy using a multi-layer approach that distinguishes between sunlit and shaded leaves, and separation of PAR into direct and diffuse components (Kropff and van Laar, 1993; Spitters et al., 1986; Supit and Van der Groot, 2003). Radiation penetration is accounted by this multi-layer approach using the concept of light attenuation in canopy (de Wit, 1965). Decline in radiation flux is a measure for its absorption by the leaf layers and thus a derivative of light attenuation equation describes the relationship between light absorption by a layer of crop canopies and light above this layer (Spitters, 1986). This approach considers extinction coefficient for direct radiation to change throughout the day as influenced by the diurnal changes in solar elevation.This multilayer approach to scale up leaf photosynthesis to the canopy level is based on the following steps:
(1) Incident PAR is separated into direct and diffuse components following approach by Spitters et al. (1986).
(2) Cumulative LAI from the top to the bottom of the canopy is calculated at various reference heights in the canopy. There are eleven reference heights (relative to the plant height) from 0 (bottom of canopy) to 1 (top of canopy) each with 0.1 unit interval. Cumulative LAI at a given relative height is calculated as:
![]() (29)
(29)
where l is cumulative LAI at relative height hr from the top to the bottom of the layer, aLD and bLD are leaf density parameters. aLD is related to the inverse of relative height in which maximum leaf area density occurs while bLD controls the spread of leaf density along the height of the canopy (Kropff and van Laar, 1993). Leaf area density at a given height is calculated using the derivative of Eq. 29:
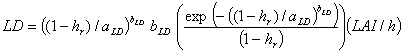 (30)
(30)
Where LD is leaf area density (cm-1) and h is absolute canopy height (cm). Rate of increase in plant height is simulated as function of cumulative f(T), where f(T) is temperature function (Wang and Engel, 1998):
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
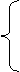
![]()
![]() (34)
(34)
![]()
where h is the canopy height (cm) at the current time, hi-1 is the canopy height (cm) at the previous time, dh/dxh is rate of change in h per change cumulative f(T). ah, bh, and ch are logistic equation parameters for canopy height and di is the time step for plant height simulation (day). xh is cumulative f(T) since emergence. Tmin, Topt, and Tmax are minimum, optimum, and maximum temperatures (C) for plant height expansion, respectively. T is mean daily temperature (C). The canopy structure is assumed to stays constant throughout the growing season.
(3) PAR absorption by sunlit and shaded leaves in each layer in the canopy is calculated following the approach given in Kropff and van Laar (1993), which applies the Beer-Lambert law of light attenuation in the canopy. Intercepted PAR (IPAR) at a given relative height is calculated as:
![]() (35)
(35)
where r and k are reflection and extinction coefficients, respectively. Reflection of the incoming PAR is influenced by the solar elevation angle according to Goudriaan (1977):
![]() (36)
(36)
where r is the reflection coefficient of the incoming PAR, s is the scattering coefficient and b is the solar elevation angle (radians). Solar elevation angle is simulated based on the Michalsky (1988) approach which provides an accurate approximation to the more complex method used by US Naval Observatory.
Vertical light attenuation by the canopy is related to the amount of light being absorbed at the corresponding layers and thus PAR absorption (APAR) at a given relative heights can be calculated as the rate of change of intercepted PAR per rate of change in LAI at a relative height (LAIrh), which is the first derivation of equation 35 (Boogard et al., 1998):
![]() (37)
(37)
By the time radiation enters the canopy, the direct beam is further partitioned into the non-scattered and scattered components. Therefore, Eq. 37 can be partitioned into absorption of the diffuse, scattered direct beam, and the non-scattered of the direct beam:
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
where the APAR terms indicate absorbed radiation flux (mmoles m-2 s-1), k terms indicate extinction coefficients, and PAR terms indicate incident radiation flux (mmoles m-2 s-1). The subscript u, w, and j represent diffuse, scattered direct beam, and the non-scattered direct beam, respectively. The extinction coefficient for diffuse radiation (ku) is given as a model parameter (0.6). The extinction coefficients associated with direct and non-scattered of direct beams are calculated following Supit and Van der Groot (2003):
![]() (41)
(41)
![]() (42)
(42)
where s is the scattering coefficient (given as a model parameter of 0.2), and b is the solar elevation angle (radians).
Shaded leaves absorb diffuse and the scattered portion of direct beam radiation, while sunlit leaves also absorb direct beams perpendicular to the leaf surface at the surface of the canopy:
![]() (43)
(43)
![]() (44)
(44)
where APARshd and APARsun are PAR absorbed by shaded and sunlit leaves, respectively (mmoles m-2 s-1). The proportion of sunlit leaves (gsun) in a given relative height is calculated as a function of the extinction coefficient for the non-scattered direct beam and the cumulative LAI from the top to the bottom of canopy according to Supit and Van der Groot (2003):
![]() (45)
(45)
(4) Photosynthesis rate for a given relative height is calculated accounting for PAR absorption by sunlit and shaded leaves, and leaf area density, and then integrated over the canopy:
![]() (46)
(46)
Sunlit leaves receive both direct and diffuse components while shaded leaves receive only diffuse radiation (Supit and Van der Groot, 2003).
The photosynthesis rate distribution along the soybean canopy height is simulated using a beta function (Wang and Engel, 1998):
 |
|||||
 |
|||||
?
?
(47)
![]()
?
where r is relative height in the canopy, rmin is the relative height near the bottom of the canopy below which photosynthesis rate reaches zero as there is no leaf present below this height, ropt is the relative height in the canopy where the photosynthesis rate is maximum as the leaf area density is maximal at this height, and rmax is relative height near at the top of canopy above which photosynthesis rate is zero as there is no leaf present above this height.
The finite integral of the beta function describing the canopy profile of photosynthesis (Eq. 47) is as follows:
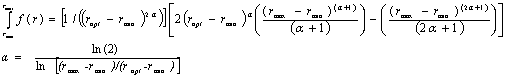 (48)
(48)
?
![]() (49)
(49)
where Pcanopy is the integrated photosynthesis rate along the height of the canopy, Propt is the maximum simulated photosynthesis rate along the canopy height (mmoles m-2 s-1). Propt is determined by comparing photosynthesis rate simulations from all eleven relative heights in the canopy. The value 0.75 is a calibration coefficient derived from comparison of the simpler versus the more complex beta function equation (Yin et al., 1995):
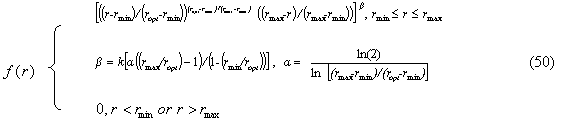
where rmin is relative height of canopy below which there is no photosynthesis rate, rmax is relative height of canopy above which there is no photosynthesis rate, ropt is relative height of canopy at which the photosynthesis rate is maximum, and k is a shape factor (a value of 2.4 was assumed in this study as it allows the best fit to the calculated photosynthesis at discrete heights in the canopy).
Details on steps for solving the integral form of the simpler beta function version are as follows:
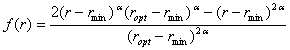
The equation can be rearranged into:
![]()
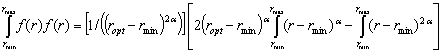
Finite integration steps:
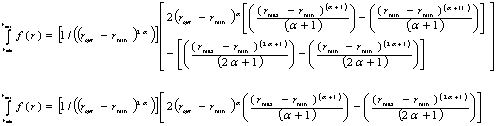
?
The photosynthesis rate for sunlit and shaded leaves is simulated as a function of absorbed PAR, [CO2], temperature, relative humidity (RH) and leaf N (g m-2) using a modified C3 plants photosynthesis model (Farquhar et al., 1980). Photosynthesis response to light and [CO2] is simulated based on the model by Farquhar et al. (1980), where the photosynthesis rate is a function of the CO2 compensation point, partial pressure of CO2, and the minimum between electron transport and rubisco limited carboxylation rates:
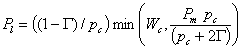 (51)
(51)
where Pl is the leaf level instantaneous gross photosynthesis (not corrected for leaf mitochondrial respiration but already accounted for photorespiration) (mmoles m-2 s-1), pc is leaf internal CO2 partial pressure (mbar), G is the CO2 compensation point (mbar), Wc is Rubisco limited carboxylation rate (mmoles m-2 s-1), and Pm is electron transport limited carboxylation rate (mmoles m-2 s-1).
The substrate input for photosynthesis in SoySim is ambient CO2 concentration ((ml l-1). Ambient CO2 and O2 concentration are converted to partial pressure values using Dalton law of partial pressure and the standard barometric formula (Miller and Anthens, 1985).
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
where pC is the ambient partial pressure of CO2 (mbar), [C] is the CO2 concentration (ml l-1), pO2is the partial pressure of O2 (mbar), [O] is the O2 concentration (ml l-1), pair is the surface air pressure (mbar), ps is the standard air pressure at sea level (1013 mbar), M is the molecular mass of air (28.8 g mol-1), g is the acceleration due to gravity (9.81 m s-1), h is site elevation above the sea level (m), R is the universal gas constant (8.3145 J mol-1 K-1) and T is the absolute air temperature (K). In this study, the value of 375 ml l-1 and 210 ml l-1 are assumed for ambient CO2 and O2, respectively. Yin and van Laar (2005) did not convert from concentration to partial pressure even though the original algorithm given by Farquhar et al. (1980) used partial pressure unit. The advantage of using partial pressure units is to account for potential differences in partial pressure of CO2 and O2 affecting carboxylation reactions due to temperature and site elevation.
Partial pressure CO2 inside the leaf is estimated from the ambient partial pressure based on the relationships described by Yin and van Laar (2005):
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
![]() (59)
(59)
![]() (60)
(60)
where Q is the ratio of internal and external partial pressure of CO2, avpd is a constant for VPD response (kPa-1), VPD is the vapor pressure deficit (kPa), kmC and kmO are the Michaelis-Menten constants for CO2 and O2, T is the air temperature (C), Tr is the reference temperature (25C), G is the CO2 compensation point (mbar), Gx is the CO2 compensation point without dark respiration (mbar), grv is the ratio of dark respiration to maximum carboxylation at ambient temperature, R is the universal gas constant (8.3145 J K-1 mol-1), grvr is the ratio of dark respiration to maximum carboxylation at reference temperature, kmCr, and kmOr are the Michaelis-Menten constants for CO2 and O2 at reference temperature. Ear, Eav, EakmC, EakmO are the activation energy for mitochondrial respiration, maximum carboxylation, kmC and kmO (J mol-1), respectively. In SoySim, VPD and T refer to air VPD and T values rather than that of leaf as in Yin and van Laar (2005).
Following Farquhar et al. (1980), the light saturated carboxylation reaction is influenced by partial pressure of CO2 and O2 with a Michaelis-Menten response:
![]() (61)
(61)
where VCmax is the maximum rubisco-limited carboxylation rate (mmoles m-2 s-1), pC,kmC, pO, and kmO are the partial pressure of and the Michaelis-Menten constants for CO2 (mbar) and O2 (mbar), respectively. Similar to kmC and kmO (Eqs. 59 and 60), VCmax at ambient temperature is described with an Arrhenius function involving an activation energy and VCmaxat reference temperature (Harley et al., 1985; Yin and van Laar, 2005):
![]() (62)
(62)
where Eav is the activation energy for VCmax (J mol-1) and VCmaxr is the maximum rubisco saturated carboxylation at reference temperature (Tr) of 25C, T is the air temperature (C), and R is the universal gas constant (8.3145 J K-1 mol-1).
Under CO2 saturation conditions, rubisco activity is limited by regeneration of ATP and NADPH that are dependent upon light driven electron transfer reactions (Farquhar et al., 1980). The function described in Harley et al. (1985) is used for the carboxylation response to light under rubisco saturated conditions:
![]() (63)
(63)
where Pm is the carboxylation rate under CO2 saturated conditions, which is an input to the Farquhar photosynthesis algorithm in Eq. 51 (mmoles m-2 s-1), a is the initial light use efficiency (mmol mol-1), Pml is the light-driven carboxylation rate at saturating light (mmoles m-2 s-1), APAR is absorbed PAR (mmoles m-2 s-1) corresponds to the sunlit and shaded components of the light absorption (Eqs. 43 and 44). Light-driven carboxylation is assumed to increase with temperature below an optimum due to an increase in enzyme activity while above the optimum, enzyme inactivation occurs (Harley et al., 1985). In SoySim, data from Harley et al (1985) and a beta function (Wang and Engel, 1998) are used to allow the light-driven carboxylation to be temperature-sensitive:
![]() (64)
(64)
where PmlT is the CO2 saturated carboxylation rate at saturating light and optimum temperature (mmoles m-2 s-1), and fp(T) is temperature function (Wang and Engel, 1998) for light-driven carboxylation (cardinal temperatures are 5, 36, 50 for Tmin, Topt, and Tmax, respectively).
N leaf (g m-2) also plays a role in determining the capacity for carboxylation (Farquhar et al., 1980; Sinclair and Horie, 1989). In SoySim, a logistic function described in Sinclair and Horie (1989) is used to account for the nitrogen relation of carboxylation under rubisco and electron transport limited:
![]() (65)
(65)
Where f(NL) is the leaf N response function for the light and rubisco carboxylation reactions, NLmax is the maximum leaf N content above which carboxylation rate reaches a plateau (g m-2), and NLcrt is critical leaf N below which carboxylation is zero (g m-2), and NL is current day N leaf (g m-2). The pattern of N leaf during the growing season was estimated based on published data (Boote et al., 1998) and assumed to be phenology-dependent. Accounting for N leaf, VCmaxr (Eq. 62) and Pml (Eq. 63) of rubisco-limited and light-driven carboxylation, respectively, are calculated as follows:
![]() (66)
(66)
![]() (67)
(67)
where VcmaxN is the maximum rubisco saturated carboxylation at 25 C and at optimum N leaf (mmoles m-2 s-1), and PmlN is the CO2 saturated carboxylation rate at saturating light, and optimum temperature and N leaf (mmoles m-2 s-1).
Photosynthesis rate (Eq. 28) is calculated based on the integrated canopy photosynthesis rate (Eq. 49) and temperature driven leaf respiration rates (Harley et al., 1985):
![]() (68)
(68)
![]() (69)
(69)
where Pt is the integrated canopy photosynthesis rate (kg CO2 ha-1 h-1), Rd is the leaf respiration rate (mmoles m-2 s-1), ard is a constant for leaf mitochondrial respiration constant (mmoles m-2 s-1), Eard is the activation energy for leaf mitochondrial respiration (J mol-1), R is the universal gas constant (8.3145 J K-1mol-1) and T is the air temperature (C).
The relationships between photosynthesis and intercepted PAR or ambient [CO2] that were derived from measurements taken in this study (as mentioned earlier) were used in these functions, while the relationship between light-saturated photosynthesis and temperature was taken from Harley et al. (1985) (Fig. 3.6). Optimal leaf N at different phenological stages was estimated from the data of Boote et al. (1998).
Simulated WDM and TDM are adjusted for abscission of petioles and leaves. The biomass of abscised petioles and leaves is simulated empirically based on field observations in the Nebraska field experiments, as a function of specific leaf area (SLA) and the rate of decline in LAI. Reduction in dry matter due to abscission of leaves and petioles is simulated as a function of specific leaf area (SLA) and the rate of decline in LAI :
![]() (70)
(70)
where Dspt is the rate of leaves and petioles abscission (kg ha-1 d-1), DLAI is the rate of decline in LAI (m2 m-2 d-1), SLA is specific leaf area (cm2 mg-1). The 10-2 term represents a unit conversion factor for SLA from cm2 mg-1 to ha kg-1. The term 0.8 suggests that not all of the dry matter in leaves and petioles are lost during senescence. Instead, as much as 20% of the dry matter is recycled thru remobilization of assimilates. SLA in eq. 70 includes petioles dry matter and is calculated as follows:
?
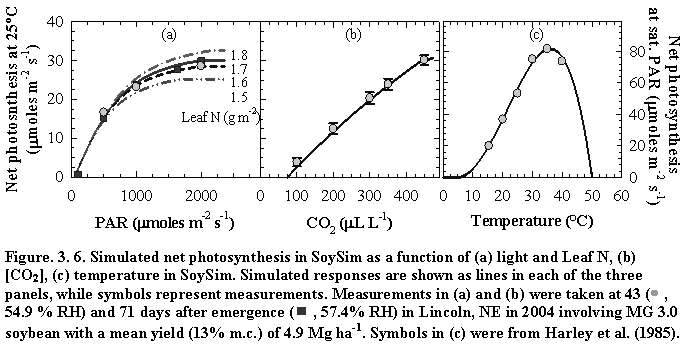
?
![]() (71)
(71)
where SLAref is phenology-dependent specific leaf area (cm2 mg-1) and f(Rs, T) is a function of solar radiation and temperature. SLA is assumed to correlate positively with mean temperature, but negatively with cumulative solar radiation (Ng and Loomis, 1984):
![]() (72)
(72)
where T is daily mean temperature during the first 20 days after emergence (C) and Rs is cumulative solar radiation at 20 days after emergence (MJ days).
Seed dry matter is simulated by estimating the number of seeds and the mean individual seed growth rate:
![]() (73)
(73)
where SDM is seed dry matter (kg ha-1), SW is mean individual seed weight (mg seed-1), Sct is number of seeds (seeds m-2) and the term 0.01 represents unit conversion factor. Seed yield at 13% moisture content is calculated assuming 3% moisture content of seed dry matter, thus seed yield = (97/87) SDM. Seeds contain about 3% residual moisture when dried to constant weight in an oven at 70C.
Number of seed is simulated as function of assimilate availability, assimilate demand, and a partitioning coefficient using a modified Charles-Edwards model (1986):
![]() (74)
(74)
![]() (75)
(75)
where DSct is rate of change in number of seeds (seeds m-2 d-1), t is time interval in days, gS is the partitioning coefficient for seeds (kg seed kg-1 aboveground biomass), F is assimilate available for growth (kg ha-1 d-1). Rms is seed maintenance respiration (kg ha-1 d-1), AdS is assimilate demands required for continuing growth of an individual seed (kg ha-1 seed-1 d-1), asctis a proportional constant (m2 d-1). Total above ground growth rate is used as an of estimate F (Egli and Zhen-wen, 1991), and gS is simulated using a Gaussian function of developmental stage:
![]() (76)
(76)
where xd is developmental progress from R1 to R7 and R8, ags, bgs, cgs are Gaussian coefficients for gS. and xd is calculated as the cumulative developmental rate from R1 to R7 + cumulative rate from R1 to R8. AdS is estimated from reproductive growth rate, which is the sum of growth rates for seed and maternal tissue of reproductive organs (flowers + pod walls):
![]() (77)
(77)
where MGR is maternal tissue (flowers + pod walls) growth rate (kg ha-1 d-1), t is time interval in days, and SGR is seed growth rate (kg ha-1 d-1). The inclusion of maternal tissue for assimilate demands is based on Sheldrakes (1979) hypothesis that pods require a small but critical amount of assimilate during initial growth (during which seed weight is negligible), followed by much greater assimilate demand for seed growth. As a result, the availability of assimilate to support both sinks, maternal tissue and seeds, determine the number of daily cohort seeds that survive and contribute to seed number. SGR in Eq. 15 is calculated as the difference between the current and previous day SDM, while MGR is simulated using the first derivative of a logistic function and developmental stages:
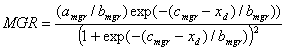 (78)
(78)
where xd is developmental progress from R1 to R7 and R8 (also used in eq 14), and amgr, bmgr, cmgr are logistic function coefficients.
Individual seed weight,SW in Eq. 73, is estimated by the relationship:
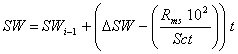 (79)
(79)
where DSW is gross rate of change in mean individual seed weight (mg seed-1 d-1) , t is time interval in days, the term i-1 represents the value of SW from the previous day, Rms is seed maintenance respiration (kg ha-1), Sct is number of seeds (seeds m-2), the tern 102 represents unit correction factor (mg kg-1 ha m-2).
DSW is simulated using the first derivative of a logistic function and developmental stages:
![]() (80)
(80)
where DSW is gross rate of change in mean individual seed weight (mg seed-1 d-1), and the other coefficients have been described previously Rms in Eqs. 75 and 79 is simulated as function of temperature, seed maintenance respiration coefficient, and SDM as follows:
![]() (81)
(81)
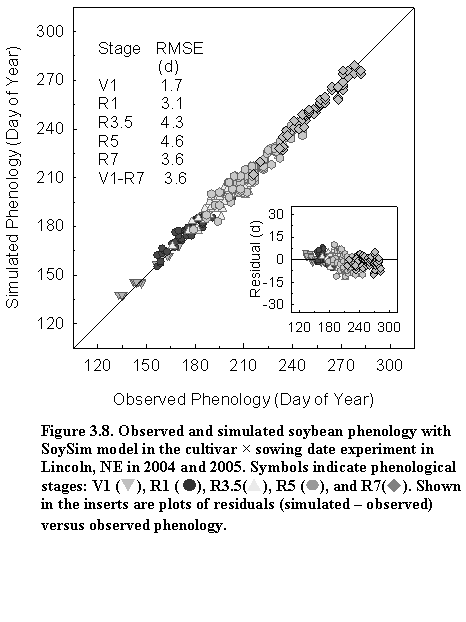
where RmsCref is seed maintenance respiration coefficient at reference temperature (kg kg-1 d-1), Q10rms is fractional change in respiration rate with a 10C increase or decrease in temperature, Trefrms is reference temperature for seed maintenance respiration (25C), SDM is seed dry matter (kg ha-1).
?
3.4. Model Validation
Validation of SoySim model has mainly been conducted for soybean grown under irrigated conditions in Corn-Soybean Belt in North America. No validation has been conducted outside this region.
3.4.1. Phenology Simulations
SoySim model reasonably simulates the patterns of vegetative development and the final number of main stem nodes for all cultivars in the planting date study in Lincoln, NE (Fig. 3.7).
Late planted soybeans developed less main stem nodes than early planted soybeans. Final main stem node number was positively correlated with duration of R1-R5 as indicated from the 2004 cultivar x sowing date study based on the actual measured values. Across all cultivars tested, the RMSE of V-stages simulation was 0.7 nodes in 2004 and 0.5 nodes in 2005. Across cultivar and sowing date, the RMSE of V-stages simulation was 1.0 d and 0.8 d in 2004 and 2005, respectively.
Using SoySim model, it was possible to evaluate the different nature of soybean node appearance and flowering in response to temperature and daylength. The delay in floral induction at later sowing dates, due to longer daylength, was not discernable in terms of duration from Emergence to R1 phase because higher temperatures later in the growing season apparently shorten the duration of the post-induction phase. Both flowering (post-induction) and node appearance respond to temperature, but only flowering (induction) responds to daylength. Therefore, comparing R1 occurrence with respect to the V-Stage allows the daylength effect on flowering (induction) to be compared between the different sowing dates without the confounding effect of temperature. The effect of daylength on floral induction was evident when R1 occurrences on different sowing dates were compared with respect to the V-Stage. Plants that were sowed on April 15, May 4, and June 17 (15.3, 15.7, and 16.2 h of daylength at V0) reached R1 at V5.7, V7.5 and V8.4, respectively.
?
A summary of six years of phenology simulation in the long-term high yield experiment in Lincoln, NE with SoySim model showed an overall RMSE of 3.6 days (Fig. 3.8). The simulation accuracy was best for unifoliate stage (V1) while least accurate for R5 stage.
Evaluation of SoySim phenology provide first indications that key model parameters needed to simulate soybean phenology on a cultivar-specific basic can be estimated from readily available cultivar information such as stem termination type and maturity group rating. This is a potential advantage of the SoySim model, particularly with regard to practical applications in which it is not possible to conduct extensive cultivar-specific model calibrations, which are required for utilizing models such as CROPGRO-Soybean.
?
3.4.2. Growth Simulations
?
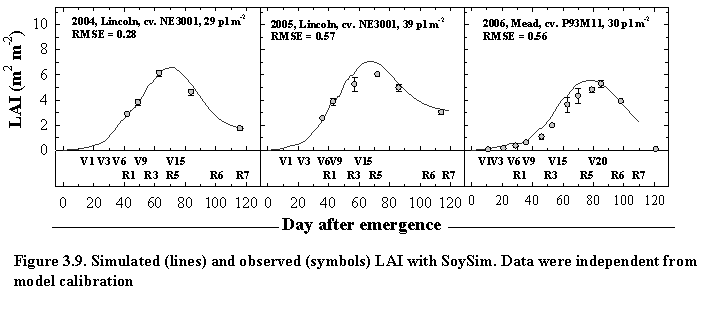
SoySim model reasonably simulated the pattern of LAI in soybean under optimum conditions at Lincoln and Mead, NE. Simulated LAI patterns included an exponential increase at the beginning of leaf growth followed by a bell-shape pattern around the peak and a decline toward physiological maturity (Fig. 3.9). Leaf expansion reached a plateau near the attainment of the maximum number of nodes. The overall RMSE value of the simulations at the two locations was 0.52 m2 m-2. For comparison, with independent data sets in central Missouri, CROPGRO model simulated soybean LAI with an overall RMSE of 1.07 m2 m-2 (Wang et al., 2003). The accuracy in LAI simulation with the SoySim model was reasonable considering that the observed LAI values ranged from 0 to 7.8 with average and maximum standard errors of 0.31 and 1.10 m2 m-2, respectively. In some cases, slight overestimation of simulated LAI was evident, typically near the peak LAI. Such overestimation of LAI indicates that under particular situations, LAI expansion becomes source limiting.
Simulation of above ground dry matter (ADM) of the validation dataset with SoySim model had an RMSE of 1.4 Mg ha-1. The SoySim model also reasonably simulated the distribution of ADM during the growing season in the validation sites (Fig. 3.10). In most cases, the simulated ADM with SoySim model was in a better agreement with the observed data, particularly later in the season, Growth simulation with SoySim involved a late season decline in ADM (between R7 to R9). Such ADM decline contributed by the abscission of leaves and petioles and to a small degree also by the attrition of plant population density (Setiyono et al., 2008; Specht et al., 2006).
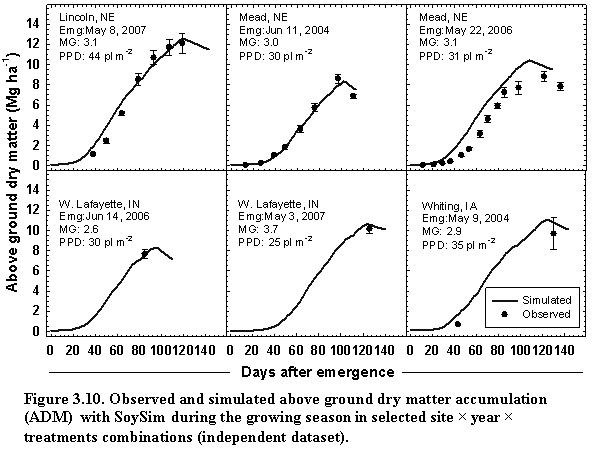
?
Simulation of seed yield at the validation sites with SoySim gave RMSE value of 0.46 Mg ha-1, (Fig. 3.11). Positive ME values indicate that simulated seed yields were, on average, overestimated by the model. Differences in observed seed yields in these studies were primarily due to different sowing-date treatments at some of the sites. Greater yields were associated with earlier sowing date. The SoySim model simulated the effect of sowing data reasonably well as indicated by the close agreement between the linear regression line and the 1:1 line.
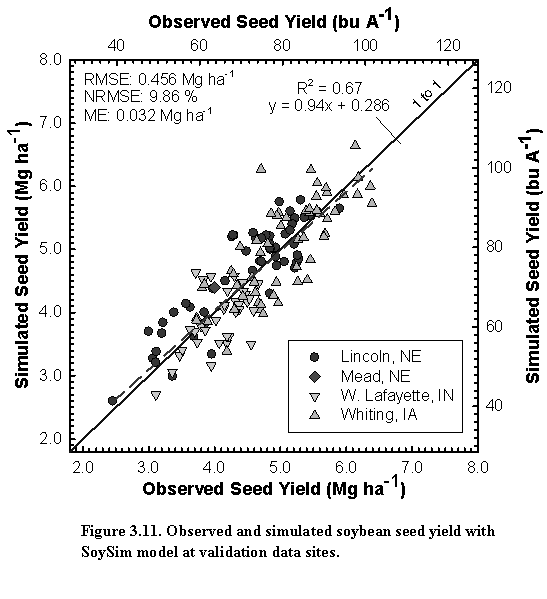
An example of application of SoySim is to access year-to-year variability of soybean yield potential. The model produced a reasonable prediction of year-to-year yield variation at the long-term high-yield experiment at the University of Nebraska-Lincoln (Fig. 3.12). It is important to access such yield variation because this yield ceiling to some degree influence other statistical yield measures such as state average yield and national average yield.
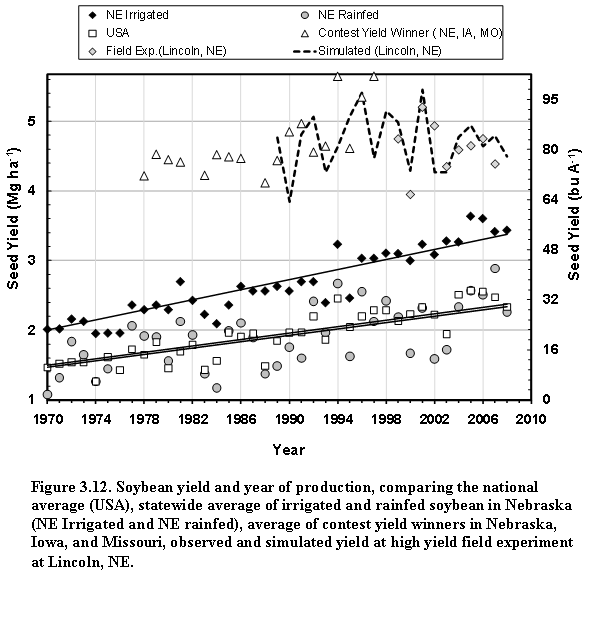
?
In addition to predicting yield in the current growing season, phenology simulation by SoySim can assist soybean grower in various management practices such as timing of fungicide application, weed control, nutrient application. With the current season simulation, the model also provides irrigation recommendation based up-to-date actual weather and thereafter based on best-yield scenario driven by combination of actual and historical weather data.
?
3.5. Uncertainties and Future Improvements
This section provides a brief summary of major uncertainties or weaknesses in the SoySim model that will have to be addressed in future research and, hopefully, can be overcome in subsequent model releases. Users should always be aware that a crop simulation model is not likely to predict growth and yield under all possible circumstances and that some applications may require a certain degreed of local model adaptation. Major known issues are:
?????? In SoySim model, only two types of stem termination were considered (indeterminate and semi-determinate). Stem termination types in soybean germplasm collections, however range qualitatively from very determinate to very indeterminate (Bernard et al., 1998). Quantification of the effect of genes such as Dt1/dt1 and Dt2/dt2 (Bernard, 1972) and dt1-t (Thompson et al., 1997) on the stem termination habit in soybean will be of future interest as it may lead to a more detailed parameterization of node appearance simulation in order to extend application of SoySim to a wider selection of stem termination types.
?????? Maturity group ratings are by themselves of a more qualitative nature and they may vary depending on the experimental procedures used to assign a MG to a commercially available soybean variety. It remains to be seen whether the empirical relationships established for estimating phenology parameters hold for an even wider range of maturity group ratings grown under widely differing conditions and whether the relationships can be linked to the genes controlling flowering and maturity in soybean such as E1/e1 and E2/e2 (Bernard, 1971; McBlain et al., 1987), E3/e3 (Buzell, 1971; McBlain et al., 1987), E4/e4 (Buzell and Voldeng, 1980), E5/e5 (McBlain and Bernard, 1987), E6/e6 (Bonato and Vello, 1999), and E7/e7 (Cober et al., 2001).
?????? The model currently does not simulate growth with water-limitation to growth. Such limitation, especially early in the season could be beneficial due to restriction of leaf expansion early in the season and thus allowing the plants to conserve water later by having smaller leaves size.
?????? SoySim does not account for effects of varying row spacing on growth and yield. Our experimental data indicates that a narrow row spacing tends to mimic a higher population density in regards to greater LAI and biomass accumulation and to some degree also yield potential.
?????? In stress environments, under-prediction of LAI is likely to have a larger impact on simulated yield than in favorable environments.
?????? The original development and validation of SoySim model was mainly done using data sets from the U.S. Corn Belt in the North Central USA. Because the model is based on process-based descriptions of crop growth and development it is expected to perform well in a wide range of environments. Nevertheless, caution should be exercised when using SoySim model outside the U.S. Corn Belt because this may require changes in some of the default model parameters.
Future model updates and improvement will focus on (i) incorporating water-limited growth, (ii) adding a module for simulating carbon and nitrogen turnover from crop residues and the soil organic carbon and nitrogen balance.
?
4. Software Development
SoySim software (Windows-based) was written in Object Pascal programming language using the Delphi 2007 for Win32 Integrated Development Environments (IDE). The model prototype and its various components including phenology, daily to hourly weather data conversion, and leaf photosynthesis were written and tested in C++ programming language using the jGRASP version 1.6.4 (Auburn University 1999-2003) and Microsoft Visual Studio.NET IDEs.
References
?
Bernard, R.L., 1971. Two major genes for time of flowering and maturity in soybeans. Crop Sci. 11, 242-244.
Bernard, R.L., 1972. Two genes affecting stem termination in soybeans. Crop Sci. 12, 235-239.
Bernard, R.L., Cremeens, C.R., Cooper, R.L., Collins, F.I., Krober, K.L., Athow, K.L., Laviolette, F.A., Coble, C.J., Nelson, R.L. Evaluation of the USDA soybean Germplasm Collection: Maturity group 000-IV (FC 01.547-PI 266.807). USDA-ARS Technical Bulletine 1844. 1998. Washinton, DC., U.S.Gov.Print.Office.
Ref Type: Report
Bonato, E.R., Vello, N.A., 1999. E6, a dominant gene conditioning early flowering and maturity in soybeans. Genet. Mo. Biol. 22, 229-232.
Boogard, H.L., van Diepen, C.A., Rtter, R.P., Cabrera, J.M.C.A., van Laar, H.H., 1998. User's guide for the WOFOST 7.1 crop growth simulation model and WOFOST Control Center 1.5. Technical Document 52. DLO Winand Staring Centre, Wageningen, The Netherlands.
Boote, K.J., Jones, J.W., Hoogenboom, G., Pickering, N.B., 1998. The CROPGRO model for grain legumes. In: Tsuji, G.Y., Hoogenboom, G., Thornton, P.K. (Ed.), Understanding options for agricultural production. Kluwer Academic Publishers, Norwell, MA, pp. 99-128.
Bozsa, R.C., Oliver, L.R., 1990. Competitive mechanism of common cocklebur (Xanthium strumarium) and soybean (Glycine max) during seedling growth. Weed Sci. 38, 344-350.
Brown, D.M., Chapman, L.J., 1960. Soybean ecology. II. Development-temperature-moisture relationship from field studies. Agron. J. 52, 496-499.
Buzell, R.I., 1971. Inheritance of a soybean flowering response to fluorescent-daylength conditions. Can. J. Genet. Cytol. 13, 703-707.
Caba, J.M., Poveda , J.L., Gresshoff, P.M., Ligero, F., 1999. Differential sensitivity of nodulation to ethylene in soybean cv. Bragg and a supernodulating mutant. New Phytol. 142, 233-242.
Cassman, K.G., Whitney, K.R., Stockinger, K.R., 1980. Root growth and dry matter distribution of soybean as affected by phosphorus stress, nodulation, and nitrogen source. Crop Sci. 73, 17-22.
Cassman, K.G., Dobermann, A., Walters, D.T., Yang, H., 2003. Meeting cereal demand while protecting natural resources and improving environmental quality. Annual Review of Environmental Resources 28, 315-358.
Charles-Edwars, D.A., Doley, D., Rimmington, G.M., 1986. Modelling plant growth and development. Academic Press, North Ryde, NSW.
Cheng, W., Johnson, D.W., Fu, S., 2003. Rhizosphere effects on decomposition: Controls of plant species, phenology, and fertilization. Sol Sci Soc Amer. J. 67, 1418-1427.
Cober, E.R., Steward, D.W., Voldeng, H.D., 2001. Photoperiod and temperature response in early-maturing, near isogenic soybean lines. Crop Sci. 41, 721-727.
Cooper, R.L., 2003. A delayed flowering barrier to higher soybean yields. Field Crop Res. 82, 27-35.
Cregan, P.B., Hartwig, E.E., 1984. Characterization of flowering response to photoperiod in diverse soybean genotypes. Crop Sci. 24, 659-662.
de Wit, C.T., 1965. Photosynthesis of leaf canopies. Agr. Res. Rep. 663, 1-57.
de Wit, C.T., 1967. Photosynthesis: Its relationship to overpopulation. In: San Pietro, A., Greer, F.A., Army, T.J. (Ed.), Harvesting the sun. Academic Press, New York, pp. 315-320.
Egli, D.B., Zhen-wen, Y., 1991. Crop growth rate and seeds per unit area in soybean. Crop Sci. 31, 439-442.
Evans, L.T., 1993. Crop evolution, adaptation and yield. Cambridge University Press, Cambridge.
Farquhar, G.D., von Caemmerer, S., Berry, J.A., 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78-90.
Fehr, W.R., Caviness, C.E., 1977. Stages of soybean development. Iowa State University, Special Report 80, Ames, Iowa.
Fischer, G., Shah, M., van Velthuizen, H., Nachtergaele, F.O., 2000. Global agro-ecological assessment for agriculture in the 21st century. IIASA, Vienna.
Goudriaan, J., 1977. Crop micrometeorology: a simulation study. Simulation monographs. Pudoc, Wageningen.
Hammer, G.L., Kropff, M.J., Sinclair, T.R., Porter, J.R., 2002. Future contributions of crop modeling - from heuristics and supporting decision making to understanding genetic regulation and aiding crop improvement. Eur. J. Agron. 18, 15-31.
Hansen, J.W., 2002. Realizing the potential benefits of climate prediction to agriculture: issues, approaches, challenges. Agric. Syst. 74, 309-330.
Harley, P.C., Weber, J.A., Gates, D.M., 1985. Interactive effects of light, leaf temperature, CO2 and O2 on photosynthesis in soybean. Planta 165, 249-263.
Hesketh, J.D., Myhre, D.L., Willey, C.R., 1973. Temperature control of time intervals between vegetative and reproductive events in soybeans. Crop Sci. 13, 250-254.
Kropff, M.J., van Laar, H.H., 1993. Modelling crop-weed interactions. CAB International and International Rice Research Institute, Wallingford, Great Britain.
Mayaki, W.C., Teare, I.D., Stone, L.R., 1976. Top and root growth of irrigated and nonirrigated soybeans. Crop Sci. 16, 92-94.
McBlain, B.A., Hesketh, J.D., Bernard, R.L., 1987. Genetic effects on reproductive phenology in soybean isolines differing in maturity genes. Can. J. Plant Sci. 67, 105-116.
Michalsky, J.J., 1988. The astronomical almanac's algorithm for approximate solar position (1950-2050). Solar Energy 40, 227-235.
Miller, A. Anthens, R.A., 1985. Meteorology. In: Charles E. Merrill Publishing Company, Columbus, OH.
Ng, E., Loomis, R.S., 1984. Simulation of growth and yield of the potato crop. Center Agricultural Pub & Document, Wageningen.
Roder, W., Mason, S.C., Clegg, M.D., Kniep, K.R., 1989. Crop root distribution as influenced by grain sorghum-soybean rotation and fertilization. Sol Sci Soc Amer. J. 52, 1337-1342.
Setiyono, T.D., Weiss, A., Specht, J., Bastidas, A.M., Cassman, K.G., Dobermann, A., 2007. Understanding and modeling the effect of temperature and daylength on soybean phenology under high-yield conditions. Field Crop Res. 100, 257-271.
Setiyono, T.D., Weiss, A., Specht, J.E., Cassman, K.G., Dobermann, A., 2008. Leaf area index simulation in soybean grown under near-optimal conditions. Field Crop Res. 108, 82-92.
Sheldrake, A.R., 1979. A hydrodynamical model of pod-set in pigeon pea (Cajanus cajan). Indian J. Plant Physiol. 22, 137-143.
Sinclair, T.R., Horie, T., 1989. Leaf nitrogen photosynthesis, and crop radiation use efficiency: A review. Crop Sci. 29, 90-98.
Specht, J., Hume, D.J., Kumudini, S.V., 1999. Soybean yield potential. A genetic and physiological perspective. Crop Sci. 39, 1560-1570.
Specht, J.E., Bastidas, A., Salvagiotti, F., Shanmugasundaram, S., Liska, A.J., Dobermann, A., Walters, D.T., Cassman, K.G., 2006. Soybean yield potential and management practices required to achieve it. In: Murphy, L.S. (Ed.), Proceedings of the 2006 Fluid Forum. Vol. 23 [CD-ROM]. Fluit Fertilizer Foundation, Manhattan, KS., Manhattan, KS.
Spitters, C.J.T., 1986. Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis: Part II. Calculation of canopy photosynthesis. Agric. For. Meteorol. 38, 231-242.
Spitters, C.J.T., Toussaint, H.A.J.M., Goudriaan, J., 1986. Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis: Part I. Components of incoming radiation. Agric. For. Meteorol. 38, 217-229.
Supit, I., Van der Groot, E., 2003. Updated system description of the WOFOST crop growth simulation model as implemented in the Crop Growth Monitoring System, CGMS, applied by the European Commission. Treemail Publisher, Heelsum, The Netherlands.
Taiz, L., Zeiger, E., 1991. Plant physiology. The Benjamin/Cummings Publishing Company, Inc., Redwood City, CA.
Thompson, J.A., Bernard, R.L., Nelson, R.L., 1997. A third allele at the soybean dt1 locus. Crop Sci. 37, 757-762.
Vessey, J.K., Layzell, D.B., 1990. Regulation of assimilate partitioning in soybean. Plant Physiol. 83, 341-348.
Wang, E., Engel, T., 1998. Simulation of phenological development of wheat crops. Agric. Syst. 58, 1-24.
Wang, F., Fraisse, C.W., Kitchen, N.R., Sudduth, K.A., 2003. Site specific evaluation of the CROPGRO-soybean model on Missouri claypan soils. Agric. Syst. 76, 985-1005.
Watt, M., Evans, J.R., 2003. Phosphorus acquisition from soil by white lupin (Lupinus albus L.) and soybean (Glycine max L.), species with contrasting root development. Plant Soil 248, 271-283.
Williams, L.E., DeJong, T.M., Phillips, D.A., 1981. Carbon and nitrogen limitations on soybean seedling development. Plant Physiol. 68, 1206-1209.
Yin, X., Kropff, M.J., McLaren, G., Visperas, R.M., 1995. A nonlinear model for crop development as a function of temperature. Agric. For. Meteorol. 77, 1-16.
Yin, X., van Laar, H.H., 2005. Crop system dynamics. An ecophysiological simulation model for genotype-by-environment interactions. Wageningen Academic Publishers, Wageningen, The Netherlands.
?
?